Александр Полулях - Грохочение угля

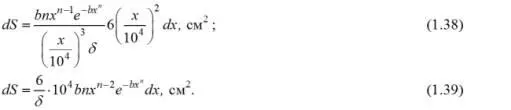
Общая поверхность частиц в классе – x 2+x 1, содержащемся в 1 г материала,

После подстановки в уравнение (1.40) получим

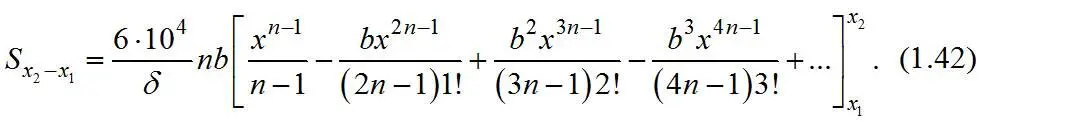
В пределах крупности от x 2=x m до x 1=1 мк вычисленная поверхность относится к классу крупности – x m+1 , содержащемуся в 1 г материала, и, следовательно, поверхность классов крупнее x m и мельче 1 мк не учитывается, что вносит некоторую ошибку в расчет.

Выход класса -1 мк составит

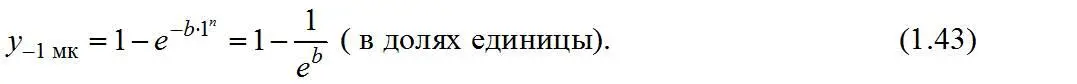
Для расчетов x m принимают исходя из выхода класса, равного 0,1 %, т. е.

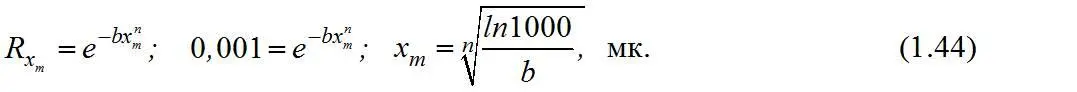
Число кубических частиц класса – x 2+x 1 в 1 г пробы по формуле (1.37) будет равно

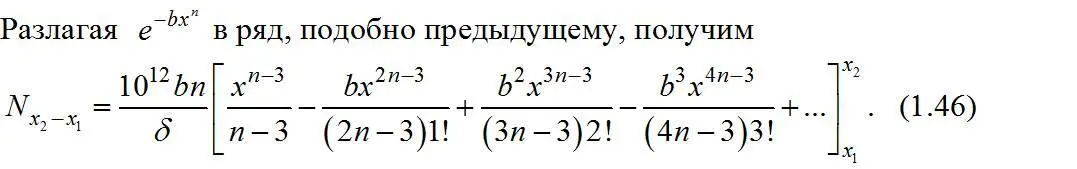
Уравнение Годэна-Андреева суммарной характеристики крупности «по минусу»

где y – суммарный выход класса минус x мк, в долях единицы; x m – максимальный размер зерна (мк), теоретически соответствующий выходу y=1; k – коэффициент, равный тангенсу угла наклона прямой суммарной характеристики по минусу в логарифмических координатах.

Уравнение кривой распределения

Число зерен в бесконечно узком классе, содержащемся в 1 г материала,

Поверхность частиц бесконечно узкого класса, содержащегося в 1 г материала,

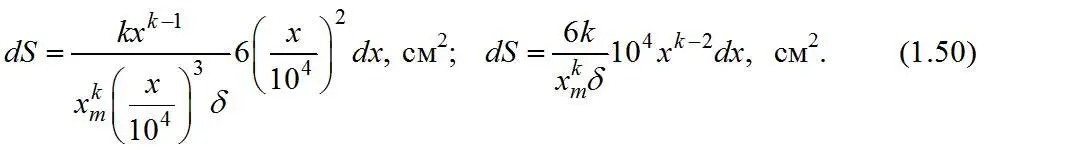
Общая поверхность частиц в классе – x 2+x 1 , содержащемся в 1 г материала,

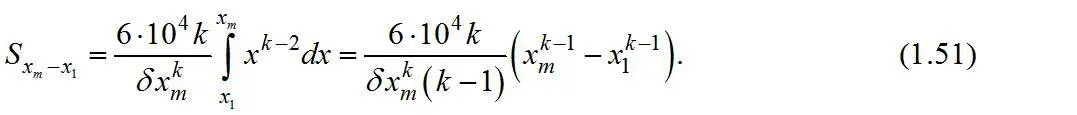
Число частиц в классе – x 2+x 1 , содержащемся в 1 г материала,

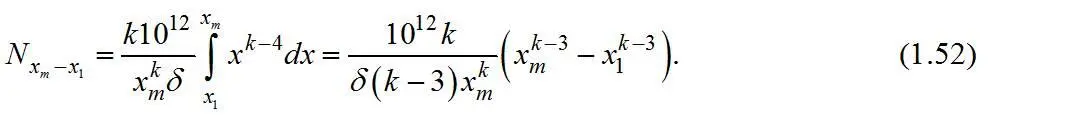
Поверхность и число частиц вычисляются по уравнению суммарной характеристики крупности при некоторых допущениях, вследствие чего расчетные показатели отличаются от действительных и могут быть использованы лишь для целей сравнения.

Основные условности, принимаемые в расчетах:

1) недостаточно обоснованно назначается предельная минимальная крупность частиц; некоторые исследователи считают, что мельчайшие частицы, получаемые при измельчении материала, не должны быть мельче 5-10 Å (1 ангстрем, обозначаемый 1 Å, равен 10 -7мм), что соответствует размеру элементарного кристалла кварца, другие полагают возможным принять за размер мельчайшей частицы 0,1 или 1 мк, учитывая малую вероятность измельчения более мелких частиц;

2) форма частиц принимается за куб или шар; действительная форма частиц отличается от правильной и для различных материалов и крупностей классов поправка на форму частиц оказывается разной.

При измерении поверхности частиц некоторых материалов газоадсорбционным методом получены отношения измеренной поверхности к теоретически вычисленной по среднему диаметру частиц, принятых за шары (табл. 1.7). На основании этих измерений при вычислении поверхности частиц мельче 0,1 мм рекомендуется принимать поправочный коэффициент 1,75 в пределах колебаний 1,3–2,6. Для угольных порошков – коэффициент 1,75 в пределах колебаний 1,6–2,0 [5];

Таблица 1.7

Значение коэффициента, учитывающего форму частиц различных материалов при вычислении их поверхности

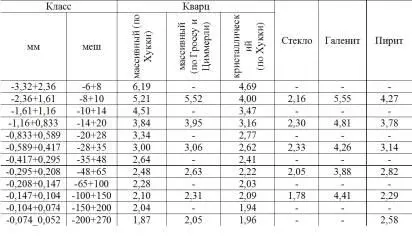
3) при вычислении по уравнению Розина-Раммлера приходится условно назначать максимальную крупность частиц, так как соответствующая кривая имеет бесконечную ветвь и нулевой выход соответствует бесконечной крупности частицы;

4) по всему ряду крупности для материала принимается постоянная плотность.

Сыпучий материал, состоящий из смеси частиц разных размеров, можно рассматривать, как некоторый статистический коллектив. Средний диаметр смеси частиц, как и всякое среднее, определяется по правилам математической статистики. Средний аргумент x , по рассматриваемому определяющему свойству , коллектива S называют одинаковое для всех членов коллектива значение аргумента x , которое им можно придать, не изменяя определяющего свойства коллектива.

Для отображения определяющего свойства в среднем диаметре необходимо, чтобы усредненный коллектив со средней величиной аргумента x=D 1,D 2…D n в отношении этого свойства ничем не отличался от эмпирического x=d 1,d 2…d n . Если точно установлено определяющее свойство, которое необходимо сохранить при усреднении, то принципиально задача определения среднего диаметра частиц решается просто: выбранное определяющее свойство выражают функцией f(d) переменного от класса к классу диаметра частиц d и той же функцией f(D) искомого среднего диаметра частиц D , который является величиной, постоянной для всех классов.

Определяющее свойство при усреднении должно остаться неизменным, следовательно,

Решая это исходное уравнение относительно D , получаем надлежащую для данного конкретного случая формулу исчисления среднего диаметра.

Обозначим через: w – весовой выход класса, n – число частиц в классе, d – средний диаметр частиц класса, D – средний диаметр частиц всей смеси. Если диапазон изменения крупности частиц в пределах класса достаточно узкий и модуль классификации не превышает 1,414, то с достаточной точностью можно принять