Александр Полулях - Грохочение угля

где d 1 и d 2 – диаметры частиц, ограничивающих класс. Примем для простоты вычислений, что все частицы имеют правильную кубическую форму и одинаковую плотность, тогда

где δ – плотность частиц (постоянная по всем классам при мономинеральном материале).

Рассмотрим на примерах вывод формул среднего диаметра с сохранением определяющего свойства при усреднении.

а) По числовому распределению частиц . Объем коллектива – число всех частиц Σn. Предположим, что определяющим свойством является поверхность всех частиц:

для реальной смеси

для усредненной смеси

Должно существовать равенство

Откуда средний диаметр, обеспечивающий сохранение при усреднении поверхности всех частиц будет исчисляться по формуле

т. е. как среднее квадратичное, взвешенное по числу частиц.

б) По весовому распределению частиц . Объем коллектива – вес всех частиц Σ w . Определяющее свойство остается то же самое – поверхность всех частиц:

для реальной смеси

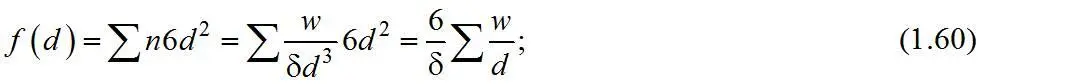
для усредненной смеси

Должно существовать равенство

откуда

т. е. средний диаметр исчисляется как среднее гармоничное, взвешенное по весовым выходам классов.

Пористостью материала называется отношение объема твердой части частицы материала к объему, занимаемому частицей [2].

Пористость является физической характеристикой твердого тела.

Порозностью материала называется отношение объема пустот между частицами материала к объему, занимаемому материалом [6].

Порозность является характеристикой сыпучего материала, указывает на степень удаления частиц друг от друга и зависит от гранулометрического состава материала и способа укладки частиц.

Порозность определяется по уравнению [6]

где m – порозность в долях единицы; α,γ – углы пространственного элемента (рис. 1.15).

На рис. 1.15 показаны виды укладки частиц шарообразной формы, а в табл. 1.8 приведена их характеристика [7].

Формула (1.64) показывает, что порозность материала, состоящая из частиц одинакового размера, не зависит от диаметра последних, а зависит лишь от вида укладки и может изменяться от 0,259 до 0,476.

Таблица 1.8

Характеристика видов укладки шарообразных частиц

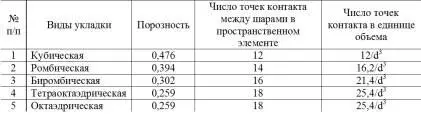
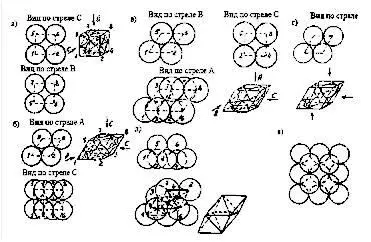
Рис. 1.15. Типы укладок слоя шаров:

а – кубическая; б – ромбическая; в – биромбическая; г – тетраоктаэдрическая; д – тетраоктаэдрической укладки; е – октаэдрическая укладка.

В табл. 1.9 приведены результаты определения порозности моноклассов различных материалов по данным [6].

В практике наиболее простым и достоверным [11] методом определения порозности является метод, при котором порозность определяется через насыпную массу виброуплотненного материала, и плотность частиц материала по формуле

где γ н – насыпная масса материала в виброуплотненном состоянии, кг/м 3; δ – плотность частиц материала, кг/м 3.

Естественно, наиболее устойчивая форма укладки октаэдрическая, для которой порозность равна 0,259. При этой геометрии шары имеют наибольшее количество точек соприкосновения, обеспечивающих их поддержку со всех сторон. В то же время кубическая и все промежуточные формы укладок менее устойчивы. Очевидно, что при любом сотрясении частицы будут стремиться занять наиболее устойчивую форму укладки, при которой порозность будет наименьшей. Однако при размещении большого количества частиц потребуется высокое совершенство укладки отдельных единиц, чего нельзя получить в естественных условиях. В естественных условиях следует ожидать образование групп, в которых размещение частиц будет беспорядочным и, где порозность будет иметь величину большую, чем 0,259.

Таблица 1.9

Значения порозности материалов после их виброуплотнения

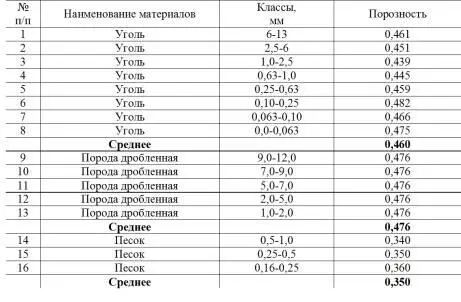
Для моноклассов различных зернистых материалов следует ожидать, что их порозность будет находиться между теоретическими значениями 0,26 и 0,48.

Полидисперсные материалы обладают меньшей порозностью, чем отдельные классы этого материала. Это объясняется тем, что меньшие по размеру частицы заполняют пространство между большими, тем самым уменьшают объем межчастичных пустот.

Из формулы (1.65) следует, что насыпная масса материала тем больше, чем меньше его порозность. Этим и определяется важность изучения порозности материалов при подготовке шихты к коксованию, при подготовке заполнителей бетона, для асфальтодорожного покрытия.

Данные табл. 1.8 показывают, что порозность различных моноклассов одного и того же материала не зависит от диаметра частиц и практически одинакова. При этом полученные величины порозности находятся в пределах теоретических значений. Различие в порозности между различными материалами – углем, породой, песком – объясняются различной формой частиц (коэффициент формы соответственно равен 0,57; 0,55 и 0,74. Моноклассы материалов, частицы которых более округлы, например, песка, укладываются наиболее плотно, в результате чего величина порозности таких материалов ниже, чем у материалов с угловатыми формами частиц.