Владимир Трошин - Со спичками не шутят

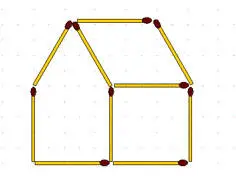
2-83.Дом. Из спичек построен дом. Переложите 2 спички так, чтобы дом повернулся другой стороной (фасадом направо).

2-84.Летучая мышь (рис. слева ниже). Переложите 3 спички так, чтобы мышь летела в противоположную сторону.

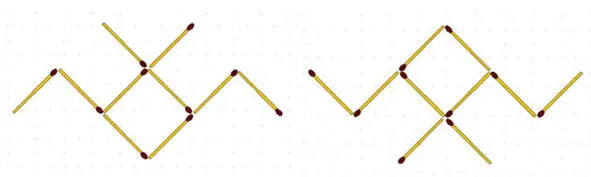
Рак (рис. справа выше). Эта задача может быть представлена в другом варианте. Спичечный рак ползёт вверх. Переложите 3 спички так, чтобы он пополз вниз.

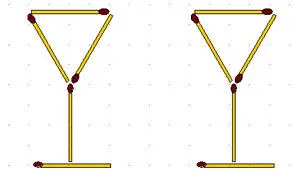
2-85.Рюмки. Две рюмки составлены из 10 спичек. Переложите 6 спичек так, чтобы получился дом.

2-86.Флюгер (рис. ниже слева). Переложив 4 спички, превратите флюгер в дом.

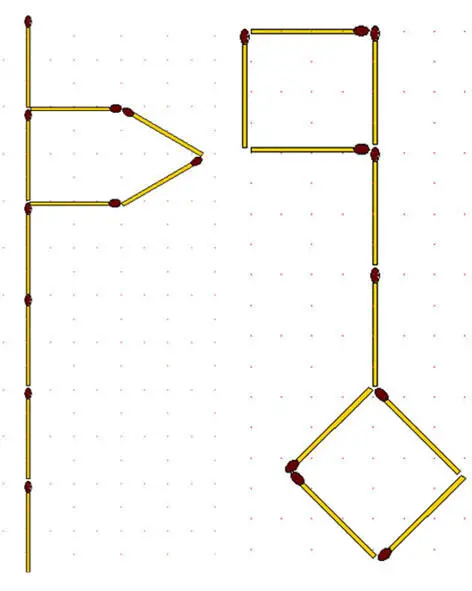
2-87.Ключ (рис. выше справа). Переложив 4 спички, превратите ключ в 3 квадрата.

2-88.Храм. Этот греческий храм сложен из 11 спичек.

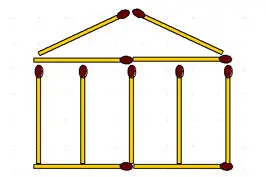
Требуется:

а) переложить 4 спички так, чтобы получилось 15 квадратов;

б) переложить 2 спички так, чтобы получилось 11 квадратов.

2-89.Лампа. Переложив 4 спички (рис. слева ниже), получите из настольной лампы 5 равновеликих треугольников.

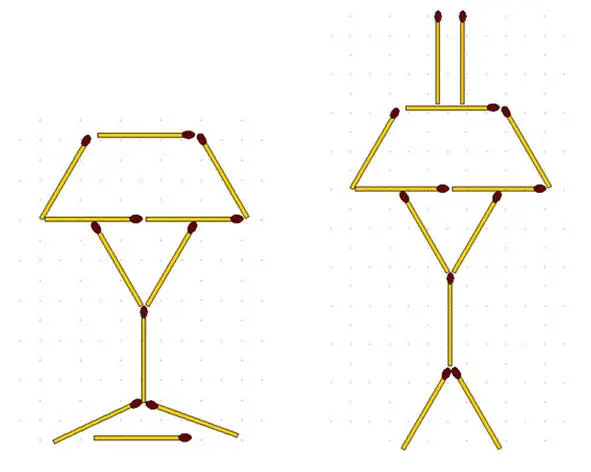
2-90.Лампа-2 (рис. справа выше). В лампе, составленной из 12 спичек, переложите 3 спички так, чтобы получилось 5 равных треугольников.

2-91.Звезда и крест. Переложите у этой 12-конечной звезды 4 спички так, чтобы получился 4-конечный георгиевский крест.

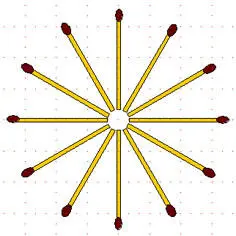
2-92.Кресты. Получив в предыдущей задаче георгиевский крест, переложите в нём 8 спичек так, чтобы получился крест, состоящий из 4 крестов.

2-93.Во вновь полученном кресте, переложите 8 спичек так, чтобы образовалось 4 квадрата.

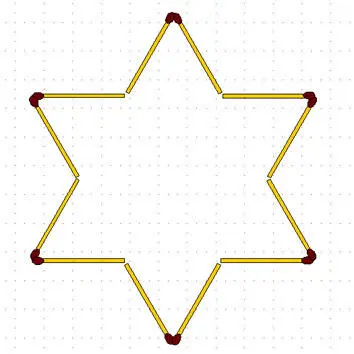
2-94.Звезда. Переложите в звезде 6 спичек так, чтобы получилось 3 равных и одинаково расположенных четырёхугольника.

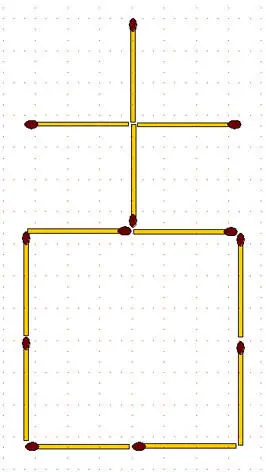
2-95.Памятник. Требуется переложить 5 спичек так, чтобы получилось 3 квадрата.

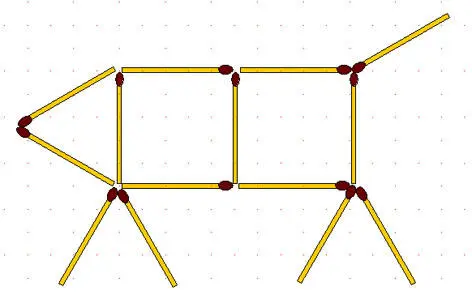
2-96.Поросёнок. Передвинув как можно меньше спичек, заставьте поросёнка повернуться в противоположную сторону.

2-97.Стрела. Из 16 спичек выложена стрела:

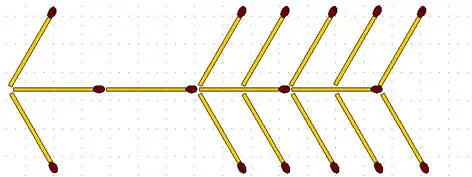
а) переложите 8 спичек так, чтобы получилось 8 равных треугольников;

б) переложите 7 спичек так, чтобы получилось 5 равных четырёхугольников.

2-98.Звезда-2. Переложите 6 спичек так, чтобы получилось 6 равных симметрично расположенных четырёхугольников.

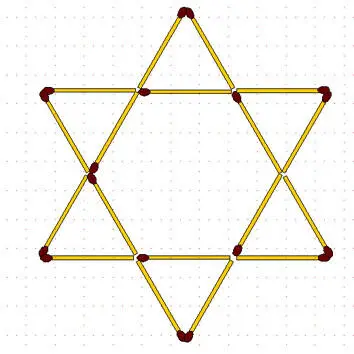
2-99.Зигзаг. Переложите 8 спичек так, чтобы получилось 2 неравных квадрата.

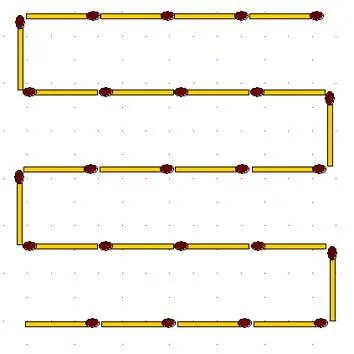
2-100.Изгородь. Переложите 14 спичек так, чтобы получилось 3 квадрата.

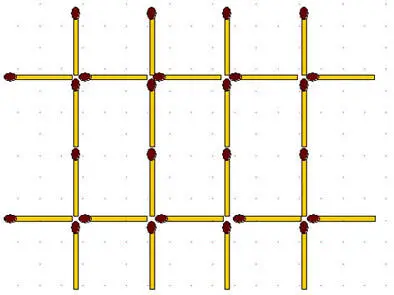
2-101.Спираль. Спираль из 35 спичек закручена против часовой стрелки. Переложите 4 спички так, чтобы получилась такая же спираль, но закрученная по часовой стрелке.

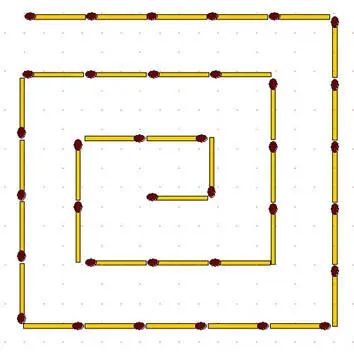
2-102.Спираль-2. В такой же спирали из 35 спичек переложите 4 спички так, чтобы получилось 3 неравных квадрата.

Раздел В.Площади фигур.

Примем за единицу длины – длину одной спички. Тогда площадь квадрата, сложенного из 4 спичек, будет составлять одну условную квадратную единицу (у. кв. ед.). Надеемся, что читатель обладает знаниями о площадях плоских фигур в объёме средней школы и ему не составит труда применить простейшие формулы для вычисления площади прямоугольника, параллелограмма, ромба, трапеции, правильных многоугольников или фигур составленных из этих простейших.

2-103.На рисунке изображен четырёхугольник из 6 спичек, площадь которого вдвое больше площади квадрата со стороной, равной одной спичке. Задача состоит в том, чтобы изменить форму четырёхугольника, не изменяя его периметра, так, чтобы площадь уменьшилась:

а) вдвое; б) вчетверо.

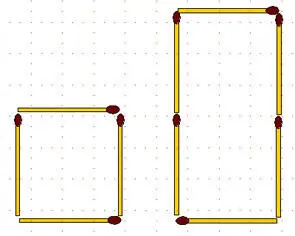
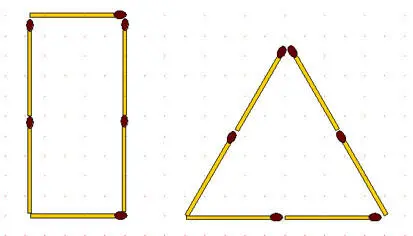
2-104.Из 6 спичек сложены прямоугольник и равносторонний треугольник. Периметры этих фигур одинаковы, а у какой больше площадь?

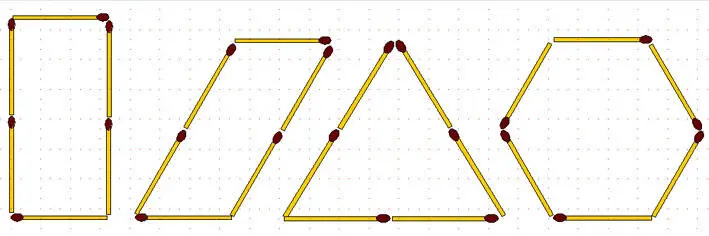
2-105.Из 6 спичек можно составить различные фигуры. Некоторые из них изображены на предыдущем рисунке. Спрашивается, у какой фигуры, составленной из 6 спичек, самая большая площадь?

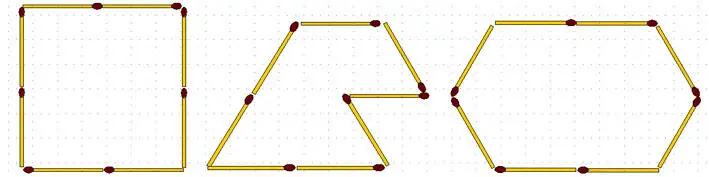
2-106.Из 8 спичек можно составить ещё больше различных замкнутых фигур. Некоторые из них представлены на рисунке. Площади фигур различны. Сложите из 8 спичек фигуру с наибольшей площадью.

2-107.С помощью 4 спичек можно построить квадрат площадью 1 у. кв. ед. Сколько спичек потребуется, чтобы построить фигуру, имеющую площадь не менее 10 у. кв. ед.?

2-108.Дано 12 спичек. Требуется сложить фигуру, имеющую площадь 3 у. кв. ед. (Исключим простейший случай, показанный на рисунке к задаче 2-37).

2-109.Из 12 спичек можно сложить фигуру площадью 9 у. кв. ед. Переложив 8 спичек, уменьшите площадь на 4 у. кв. ед.

2-110.Постройте из 12 спичек фигуру площадью ровно 4 у. кв. ед.