Владимир Трошин - Со спичками не шутят

2-111.Из 20 спичек составлены два прямоугольника: один из 14 спичек, а другой – из 6. Ясно, что площадь второго прямоугольника в 3 раза меньше площади первого. Сломайте данные фигуры и составьте новые, снова из 14 и из 6 спичек, причём с тем же отношением площадей.

2-112.Площадь прямоугольника из 14 спичек в 3 раза больше площади прямоугольника, составленного из 6 спичек. Теперь возьмите 1 спичку в б ольшей группе, переложите её в м еньшую и с помощью 7 и 13 спичек ограничьте снова две фигуры, из которых площадь одной была бы ровно в 3 раза больше площади другой.

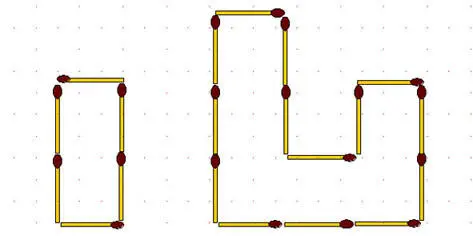
2-113.

Соотношение площадей фигур 1:3. Теперь возьмите 1 спичку в б ольшей группе, переложите её в м еньшую, и постройте новые фигуры с тем же соотношением площадей. Только сделайте это так, чтобы 12 спичек из первоначального расположения остались на своих местах.

2-114.Примем за среднюю длину спички 5 сантиметров. Сколько потребуется спичек, чтобы выложить равными квадратами со стороной в одну спичку один квадратный метр?

Раздел Г.Деление фигуры на заданные части и разное.

2-115.Данную фигуру разделите на 4 одинаковые части с помощью 5 спичек.

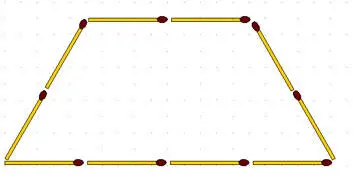
2-116.Фигуру, составленную из 16 спичек, разделите спичками на две одинаковые части.

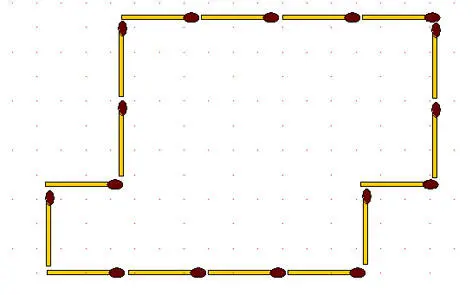
2-117.С помощью 7 спичек, разделите фигуру на 3 одинаковые части.

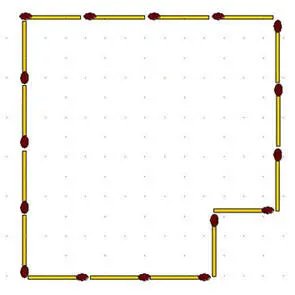
2-118.Данную фигуру (рис. ниже слева) разделите на 4 одинаковые части с помощью 8 спичек.

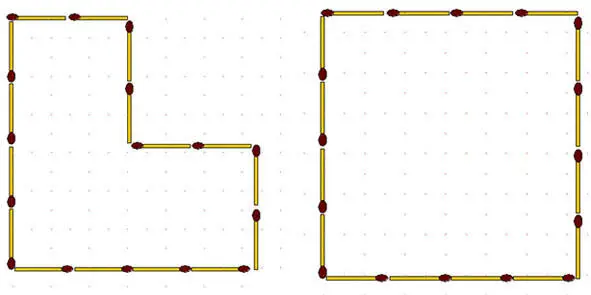
2-119.Квадрат ограничивают 16 спичек (рис. выше справа). Требуется разделить его на 4 фигуры площадью по 4 у. кв. ед. каждая с помощью 8, 10, 12 спичек (три задания). Разумеется, нельзя класть две спички на одну и ту же сторону. Труднее выполнить условие, используя 11 спичек (четвертое задание).

2-120.Выложенные в форме квадрата 16 спичек представляют изгородь двора. Часть площади двора занята домом, изображенным в виде квадрата из 4 спичек. Остальную часть двора требуется разделить при помощи 10 спичек на 5 участков, одинаковых по форме и по площади.

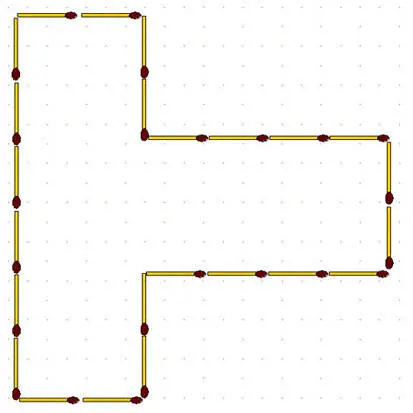
2-121.Данную фигуру разделите на 4 одинаковые части с помощью 8 спичек.

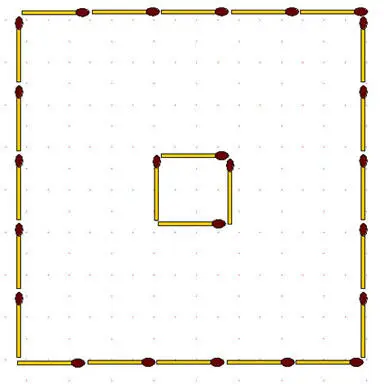
2-122.Сад, очертание которого изображено 20 спичками, и в середине которого находится дом квадратной формы, требуется:

а) разделить 18-ю спичками на 6 равновеликих и одинаковых по форме частей;

б) разделить 20-ю спичками на 8 одинаковых частей.

Раздел Д.Различные дополнения к геометрии, не вошедшие в предыдущие разделы по разным причинам.

Две задачи отличаются тем, что для их формулировки и решения, кроме спичек, нужен соответствующий рисунок на бумаге.

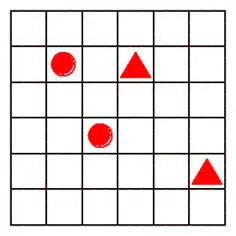
2-123.Сторона каждого маленького квадрата на рисунке, имеет длину в одну спичку. Требуется разместить ровно 26 спичек вдоль линий таким образом, чтобы они разделили весь чертёж на две части одинаковых размеров и формы, причем в одной из них должны находиться два нарисованных треугольника, а в другой – два круга.

2-124.На бумаге начерчен квадрат со стороной равной длине 4 спичек и прямыми линиями разделён на 16 меньших квадратов.

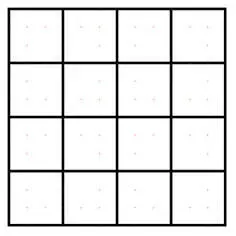
Задача состоит в том, чтобы расположить спички на листе выполняя три условия:

1) каждая спичка должна закрывать сторону одного из маленьких квадратов;

2) у каждого из маленьких квадратов ровно 2 стороны должны быть закрыты спичками;

3) спички нельзя размещать, на краю большого квадрата, то есть по внешним сторонам.

Решите ту же задачу для исходного квадрата с длиной стороны в 5 спичек.

Отдохнем от решения заданий. На уроках школьной геометрии, прежде чем решать задачи, учитель объясняет соответствующие теоремы и доказывает их. Оказывается и теоремы можно доказывать «на спичках». Очень важной для всего курса геометрии является теорема о сумме внутренних углов треугольника. Вот как можно доказать ее с помощью простой спички. Начертив на доске треугольник, положим на одну из его сторон (например, в вершине А ) спичку, направленную головкой от точки А в сторону точки В .

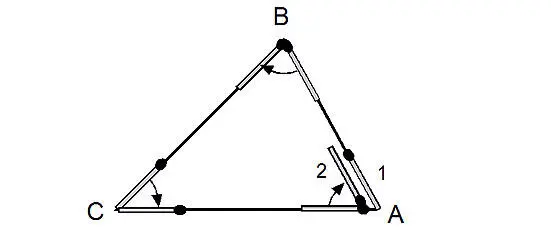
Далее, следуя рисунку, будем двигать спичку вдоль стороны, до тех пор, пока ее головка не совпадет с вершиной В . Теперь, поворачиваем спичку так, чтобы она описала угол В и расположилась вдоль другой стороны треугольника. Сдвинем теперь спичку вдоль второй стороны до следующей вершины С и поворачиваем спичку так, чтобы она описала угол С . Далее сдвинем спичку вдоль третьей стороны до исходной вершины А , поворачиваем спичку так, чтобы она описала угол А и вернулась в исходное положение, повернувшись при этом на все три угла треугольника, причем строго по часовой стрелке. В итоге она окажется совмещенной с первоначальной стороной треугольника, но ее головка «смотрит» в противоположное направление. Угол, описанный спичкой, равен сумме внутренних углов треугольника, а с другой стороны её суммарный поворот равен развернутому углу, то есть 180 0. Этот метод доказательства называется «метод скользящей спички». Им можно воспользоваться для определения суммы внутренних углов четырехугольника, он служит удобным способом измерения углов любых многоугольников с любыми сложными самопересечениями.

Серьезные рассуждения подготовили нас к серьезным задачам. Спичечный коробок по форме представляет собой прямоугольный параллелепипед.