Петр Силин - Некоторые аспекты оценки эффективности функционирования систем. Вторая редакция, исправленная и дополненная

Данное выражение (14) очень сильно напоминает второй закон Ньютона, но это не страшно.

Второй закон Ньютона говорит о том, что постоянное воздействие сообщает объектам постоянное ускорение движения (возникающее скачком), не изменяющееся за весь период приложения силы. Постоянство ускорения обеспечивает линейный рост скорости и квадратичный рост пройденного расстояния под действием силы.

С другой стороны, второй закон Ньютона говорит о том, что функциональная зависимость силы и ускорения объекта одинаковы (при постоянной массе). Но масса может в процессе движения изменяться. Если масса будет изменяться в одной и той же функциональной зависимости, что и сила воздействия, то в этом случае при любой функциональной зависимости силы ускорение будет постоянным. При анализе данного феномена период наблюдения, совпадающий с периодом существования воздействия, следует делить на интервалы, в пределах которых соотношение величины воздействия и меры инерции будет постоянно (другие варианты взаимного изменения воздействия и массы объекта требуют отдельного исследования).

В случае этого нюанса недоучет малых воздействий может привести к неправильной оценке меры инерции объекта и спектра ответа на воздействие.

Отметим, что второй закон Ньютона в своем каноническом виде применим для исследования только одного вида параметра – координаты евклидова пространства. Выражение (14) будет использоваться более широко – для исследования поведения параметров любого вида, образующих параметрическое пространство.

При этом воздействие, как векторный объект, в параметрическом пространстве распадается на субвоздействия по отдельным параметрам, это позволяет допустить, что и мера инерции, и скоростные характеристики также распадаются на частные, по видам параметров, векторы скоростей, ускорений и пройденных этапов.

1.3.10. Скорость движения.

При рассмотрении идеальных систем вполне допустимо считать, что объект переходит из одного состояния в другое мгновенно, что позволяет не учитывать фактор времени при анализе объектов.

Если же обратиться к реальным объектам, а возможно это придется иногда делать, то становится очевидным, что переход объекта из одного состояния в другое совершается за конечный интервал времени.

Время перехода из одного состояния в другое формируется временами изменения значений параметров, и чем медленнее способен перестраиваться тот или иной параметр, тем дольше объект будет переходить из одного состояния в другое.

Полное перестроение объекта произойдет тогда, когда требуемое значение примет параметр, которому требуется для этого наибольшее время в рамках данного этапа движения – имеется в виду, что какой-либо параметр может перестраиваться быстро, но требуется настолько большое изменение значения, в результате чего эта операция будет закончена позже аналогичных операций по остальным параметрам.

Обозначим это время как T max .

Вообще говоря, в различного вида системах, особенно технических, относительно легко определяются удельные времена изменения значений параметров, т.е. время, необходимое для изменения соответствующего параметра на определенную величину (другое наименование такого временного параметра – постоянная времени соответствующего параметра).

Существование конечного времени перехода объекта из одного состояния в другое позволяет говорить о таком факторе, как скорость движения объекта в пространстве состояний, которую можно определить стандартным образом как отношение пройденного пути S , на рисунке 9 такое расстояние обозначено как |AB|, в пространстве состояний к затраченному на это перемещение времени.

Тогда можно определить выражение для скорости перемещения объекта в пространстве состояний между двумя состояниями V :

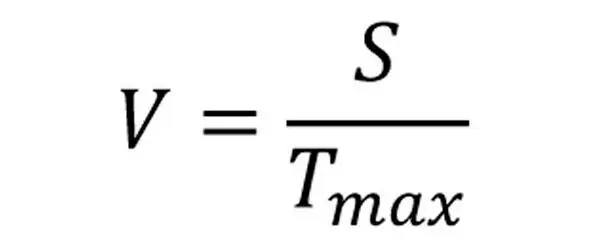
выражение 14.1

Если объект совершает многоэтапный переход в пространстве состояний или в процессе перемещения скорость перемещения в каждый момент времени не была постоянной, то можно говорить о таком показателе, как средняя скорость движения объекта в пространстве состояний.

В процессе своего генезиса любой объект, по мнению автора, выполняет две основные задачи и одну промежуточную:

– осуществляет движение в пространстве состояний по каким-либо параметрам;

– поддерживает стабильное состояние по каким-либо параметрам;

— осуществляет переход от движения к стабильному состоянию или обратно, либо изменяет режим движения.

Часто оказывается, что исполнение этих задач происходит не само собой, а за счет использования определенных свойств или параметров объекта.

Свойства либо параметры объекта, использующиеся в процессе решения тех или иных задач, в дальнейшем будут именоваться ресурсами или ресурсными параметрами. В свою очередь параметры, требующие использования ресурсов, будут именоваться ресурсозависимыми.

Использование тех или иных ресурсов в процессе решения задач сопровождается уменьшением (именно уменьшением) значений ресурсных параметров, если не производится постоянное восстановление ресурсов извне объекта. При включении таких параметров в пространство состояний в качестве координат окажется, что исполнение объектом стоящих перед ним задач приводит к смещению текущего состояния объекта относительно состояния, прогнозируемого без учета использования ресурсов.

Более того, если объект затрачивает ресурс для решения задач (движение к целевому состоянию, его удержание, старт к началу движения), то, вследствие изменения параметра ресурса и появления соответствующего смещения, объект, если не будет предпринято специальных усилий, не достигнет целевого состояния (определяемого вектором цели) в формальном смысле, а окажется в другом состоянии.

В качестве иллюстрации сказанного ниже приведен рисунок 11.

Для наглядности отображения движения в пространстве состояний за счет ресурса представляется допустимым принять тривиальную модель использования ресурсов – каждое изменение параметра, требующее затрат ресурса, на какую-либо величину (см. 9/1) сопровождается уменьшением ресурса на такую же величину (см. 10/1) в нормализованных значениях параметров (вообще говоря, каждый объект использует свои ресурсы по-своему и с присущей ему скоростью).

Обратимся к рисунку 11.

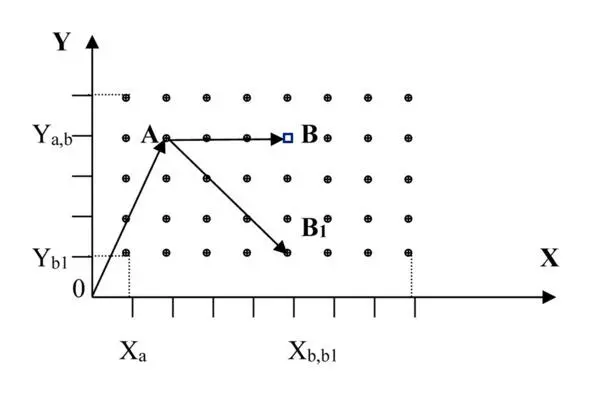
Рисунок 11. Движение с использованием ресурсов