Константин Быструшкин - Феномен Аркаима. Космологическая архитектура и историческая геодезия

Убедимся в том, что использование точки В (узла градусной сетки) не случайно. Для этого проведем геодезическую прямую ВО 1и продолжим ее далее к юго-востоку. Она пересечет другой узел градусной сетки с координатами 52°00'00" с.ш. и 61°00'00" в.д. (точка Д). По точному расчету диагональ геодезического полуквадрата (ВД) пройдет в непосредственной близости от О 1– непосредственно через геодезический знак на высоте 443,9 м. Давно понятно, что высота 443,9 м является естественным конкурентом центра О 1, но рассматривать ее в качестве альтернативы мы не будем. Это загромоздит изложение и не даст новых результатов. Проведенные расчеты показывают, что конструкторы Страны Городов предпочитали О 1.

Азимут диагонали ВД (-50° 44'18",65) очень близок величине азимута главной оси Аркаима + 50°43'. Разница в знаках (направлениях отсчета) может быть объяснена геоцентрической проекцией полуквадрата. Впрочем, в геометрии внутреннего круга Аркаима есть стенка-перегородка с азимутом (- 50°43').

Геодезический полуквадрат, который показал себя через диагональ ВД и отрезок Вх, образован меридианами 59°00'00" в.д., 61°00'00" в.д. и параллелями 52°00'00" с.ш., 53°00'00" с.ш. Меридиан 60°00'00" в.д. проходит ровно через его середину. Обозначим полуквадрат АВСД. Поверочный уральский меридиан 60°, проходящий через середину полуквадрата (делит полуквадрат на два квадрата), отстоит от египетского меридиана 30° в.д. ровно на 30° долготы или знак земного зодиака. За этим простым фактом скрывается чрезвычайно важная сущность обнаруженного геодезического феномена. Сейчас же закончим анализ линии Вх.

Определим положение точки х на меридиане 61°00'00" в.д. Линия Вх пересекает меридиан по параллели 52°46'09" с.ш. Эта точка имеет свою особенность. Чтобы ее увидеть, оценим удаление центра системы О 1от параллели 53°00'00". Удаление составит 48,407 км или 26'06" (53° – 52°33'54"). Разделим полученный отрезок пополам: (26'06" : 2 = 13'03") и прибавим половину к широте О 1(52°33'54" + 13'03" = 52°46'57" с.ш.). Таким образом, точка х очень близка к середине отрезка меридиана 61° между параллелями центра О1 и 53° (рис. 114).

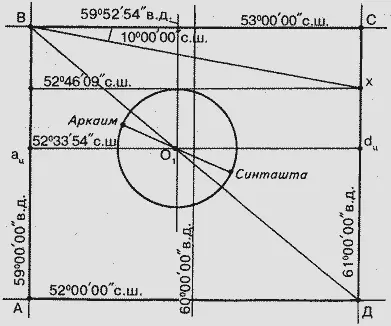
Рис. 114. Геодезический полуквадрат системы О1.

К тому же, параллель 52°46'09" пересекает меридиан центра О 1почти в том же месте, где и окружность радиуса 22,837 км (О 1– Аркаим), от О 1до параллели 52°46'09" – 22,720 км.

Рассмотрим еще один аргумент в пользу утверждения, что конструкторы употребляли геодезический полуквадрат АВСД. Этим аргументом будет геодезическая прямая, проходящая через городища Андреевское и Синташта-II.

Продолжив линию к северо-западу до меридиана 59°, мы попадем в точку а цс координатами:

59°00'00" в.д.;

52°33'54" с.ш.

Последняя параллель есть параллель центра О 1. Продолжив линию к юго-востоку до меридиана 61°, мы попадем в точку – у с координатами:

61°00'00" в.д.;

52°21'02" с.ш.

Точка у делит отрезок меридиана 61° (Дd ц) "золотым сечением":

52°33'54" – 52°00'00" = 33'54";

33'54" х ЗС = 20'57".

Параллель "золотого сечения" южной части полуквадрата 52°20'57" с.ш.; в то время как параллель точки у – 52°21'02" с.ш. Разница в 5" меридиана выразится в 152,5 м. Много это или мало?!

Продемонстрируем описанную картину в цифрах и схемах (рис. 115).

Таблица 6

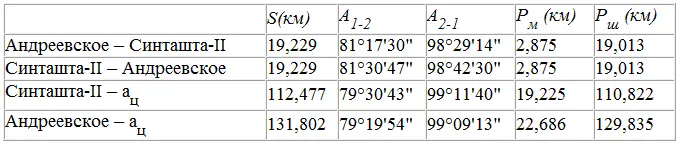
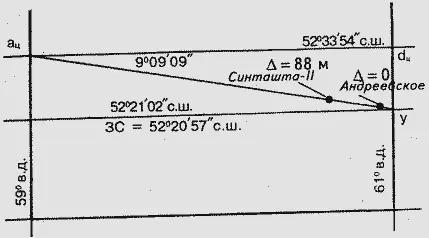
Рис. 115.

Линия а ц– у имеет азимут от меридиана точки а ц– 99°09'09" (или угол от параллели точки а ц– 9°09'09"). Сопоставив эти величины с азимутом и углом линии В-х (100°00'00" и 10°00'00"), можно заметить правильности в числах.

Параллель "городища" Андреевского близка параллели точки у, но в отличие от последней является касательной к окружности радиуса 22,837 км из центра О 1(окружности, на которой установлены Аркаим и Синташта). Удаление Андреевского от параллели центра О 1– 22,688 км. Напомним, что точка х удалена от той же параллели, но к северу, на 22,720 км. К тому же "золотое сечение южной части удалено от середины северной на 26'00". Их параллели 52°20'57" с.ш. и 52°46'57" с.ш. Вместе с тем и параллель центра О 1удалена от параллели 53° на 26'06" (26', 1). Такие результаты можно получить, если признать наличие геодезического полуквадрата и использование его в проекте. Прием продуктивен, а потому продолжим эту линию исследований.

Отметим еще одну особенность координат городищ в юго-восточной части полуквадрата. Параллель Аландского (52° 11'49" с.ш.) удалена от стороны АД на 11'49", а параллель Синташты-II (52°23'32" на 23'32", т.е. почти в два раза дальше:

703" : 1412" – 2,0085; или 11'49" ≈ 11'43" (рис. 116).

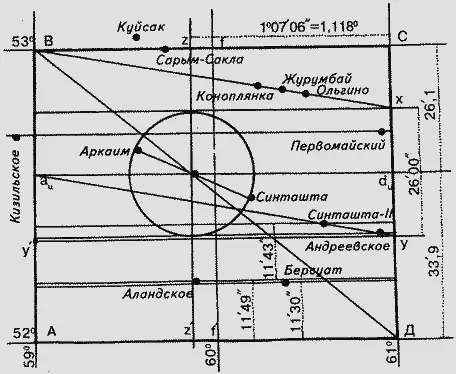
Рис. 116. Линейная структура геодезического полуквадрата ABCD.

Полезно вспомнить экзотическую меру длины в геодезии Древнего Египта – 1'09" ("минута" небесного полулоктя в 1°09'). Десять таких "минут" (11'30") очень близки удалению Берсуата от АД – 11'34".

Обнаруживается и еще один египетский геометрический инструмент – "неправильный квадрат" с отношением сторон 1 : 1,118. В нашем случае такой квадрат zCDz' вырезается в геодезическом полуквадрате АВСД меридианом центра О1 (59°52'54" в.д.). Таким образом, в системе О 1Страны Городов мы имеем великолепную гармоническую геодезическую основу:

АВСД – геодезический полуквадрат в градусной сетке от Гринвича;

ABff' и f'fCД – геодезические квадраты;

zСДz' – геодезический "неправильный квадрат".

Линия В-х содержит 5 значимых точек: точку В, точку х и три "городища" (Коноплянка, Журумбай, Ольгино). Ее угол 10°00'00" от параллели. Линия а ц– у содержит 4 значимых точки: точку а ц, точку у и два "городища" (Синташта-II и Андреевское). Ее угол 9°09'09" от параллели. Вряд ли можно доказать, что все приведенные случаи в совокупности есть случайное совпадение. Но есть и еще пример такого же рода.

Рассмотрим прямую линию а ср– С, где а ср– точка пересечения параллели геодезической середины полу квадрата со стороной АВ:

а ср: 59°00'00" в.д.;

52°30'00" с.ш.;

С: 61°00'00" в.д.;

53°00'00" с.ш.

Линия, соединяющая точки а сри С, проходит через два "городища": Аркаим и Журумбай.

Таблица 7

Такой результат хорош сам по себе, но есть возможность его улучшить. Для этого нужно сдвинуть точку а српо меридиану к северу на 30" (927 м). Обозначим новую точку – а' ср. Рассчитаем стандартные параметры от этой точки а' ср.