Стивен Вайнберг - Первые три минуты
- Название:Первые три минуты
- Автор:
- Жанр:
- Издательство:НИЦ Регулярная и хаотическая динамика
- Год:2000
- Город:Ижевск
- ISBN:5-93972-013-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Стивен Вайнберг - Первые три минуты краткое содержание
В книге крупнейшего американского физика-теоретика популярно и увлекательно рассказывается о современном взгляде на происхождение Вселенной. Описаны факты, подтверждающие модель «горячей Вселенной», рассказана история фундаментальных астрофизических открытий последних лет. С большим мастерством и научной точностью излагается эволюция Вселенной на ранних стадиях ее развития после «Большого взрыва».
В новое издание вошла также нобелевская лекция С. Вайнберга, в которой описывается история возникновения единой теории слабых и электромагнитных взаимодействий.
Для читателей, интересующихся проблемами космологии.
Первые три минуты - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Например, галактики в скоплении Девы движутся от нашей Галактики со скоростью примерно 1000 км/с. Скорость света равна 300 000 км/с. Поэтому длина волны любой спектральной линии от скопления в Деве больше своего нормального значения λ в отношении
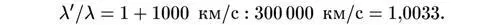
ДОПОЛНЕНИЕ 2. КРИТИЧЕСКАЯ ПЛОТНОСТЬ
Рассмотрим сферу радиуса R , внутри которой содержатся галактики. (Для целей данного вычисления мы должны выбрать R больше, чем расстояние между скоплениями галактик, но меньше любого расстояния, характеризующего Вселенную в целом.) Масса такой сферы равна ее объему, умноженному на космическую плотность массы ρ :
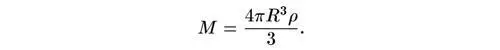
Из ньютоновой теории тяготения следует, что потенциальная энергия любой типичной галактики на поверхности этой сферы
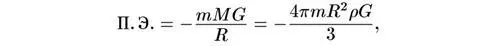
где m — масса галактики; G — ньютонова постоянная тяготения, G = 6,67 × 10 -8см 3/(г·с 2). Скорость этой галактики определяется законом Хаббла в виде
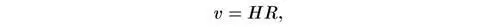
где Н — постоянная Хаббла. Следовательно, кинетическая энергия галактики равна
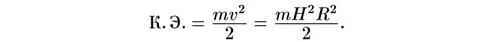
Полная энергия галактики есть сумма кинетической и потенциальной энергий:
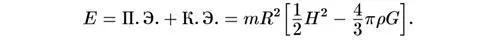
Эта величина должна оставаться постоянной в процессе расширения Вселенной.
Если полная энергия Е отрицательна, галактика никогда не может удалиться в бесконечность, так как на очень больших расстояниях потенциальная энергия становится пренебрежимо малой, и в этом случае полная энергия просто равна кинетической энергии, которая всегда положительна. Если же полная энергия Е положительна, галактика может достичь бесконечности, имея остаточную кинетическую энергию. Таким образом, условие того, что галактика имеет скорость, как раз равную скорости отрыва, заключается в том, что Е обращается в нуль, что дает
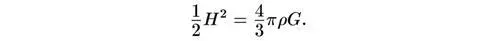
Другими словами, плотность должна иметь значение
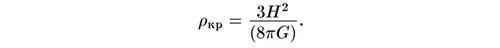
Это и есть критическая плотность. (Хотя этот результат получен здесь с использованием принципов ньютоновой физики, он на самом деле справедлив даже тогда, когда содержимое Вселенной является ультрарелятивистским, если только иметь в виду, что ρ интерпретируется как полная плотность энергии, деленная на с 2 .)
Например, если Н равна популярному в настоящее время значению 15 км/с на миллион световых лет, то, вспоминая, что световой год соответствует 9,46 × 10 12километров, мы получаем
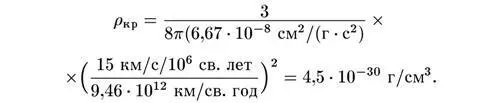
В одном грамме содержится 6,02 × 10 23ядерных частиц; такое значение теперешней критической плотности соответствует примерно 2,7 × 10 -6ядерных частиц в 1 см 3, или 0,0027 частицы в одном литре.
ДОПОЛНЕНИЕ 3. МАСШТАБЫ ВРЕМЕНИ РАСШИРЕНИЯ
Рассмотрим теперь, как меняются параметры Вселенной с течением времени. Предположим, что в момент времени t типичная галактика массы m находится на расстоянии R(t) от некоторой произвольно выбранной центральной галактики, например нашей собственной. Мы видели в предыдущем математическом дополнении, что полная (кинетическая плюс потенциальная) энергия этой галактики равна
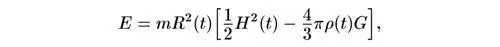
где H(t) и ρ(t) — значения постоянной Хаббла и космической плотности массы в момент времени t . Энергия должна быть всегда постоянной. Однако мы увидим ниже, что при R(t) → 0 ρ(t) увеличивается, по меньшей мере, как 1/R 3(t) , так что ρ(t)R 2(t) растет как 1/R(t) при R(t) , стремящемся к нулю. Чтобы сохранить энергию Е постоянной, два члена в скобках должны почти сокращаться, так что при R(t) → 0 мы имеем
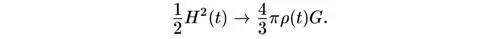
Характерное время расширения — просто обратная величина постоянной Хаббла, т. е.
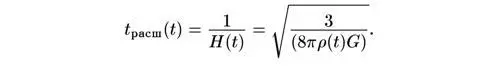
Например, в момент времени первого кадра (см. гл. V) плотность массы равнялась 3,8 тысячи миллионов грамм на кубический сантиметр. Отсюда, время расширения равнялось тогда
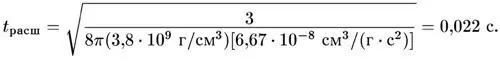
Далее, как меняется ρ(t) с изменением R(t) ? Если плотность массы определяется массами ядерных частиц (эра преобладания вещества), тогда полная масса внутри сопутствующей сферы радиуса R(t) просто пропорциональна массе ядерных частиц внутри этой сферы и, следовательно, должна оставаться постоянной:
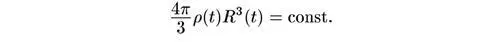
Отсюда ρ(t) обратно пропорциональна R 3(t) :
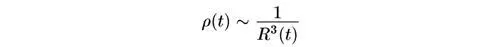
(знак ~ означает «пропорционально».) В то же время если плотность массы определяется массой, эквивалентной энергии излучения (эра преобладания излучения), тогда ρ(t) пропорциональна четвертой степени температуры. Но температура меняется как 1/ R(t) , так что ρ(t) в этом случае обратно пропорциональна R 4(t) :
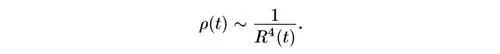
Чтобы иметь возможность одновременно рассматривать эры преобладания вещества и излучения, мы запишем эти результаты в виде
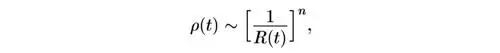
где

Кстати, заметим, что при R(t) → 0 ρ(t) растет, по меньшей мере, так же быстро, как 1/ R 3(t) , что и было указано выше.
Читать дальшеИнтервал:
Закладка:








![Стивен Вайнберг - Первые три минуты [litres]](/books/1068055/stiven-vajnberg-pervye-tri-minuty-litres.webp)

