Стивен Вайнберг - Первые три минуты
- Название:Первые три минуты
- Автор:
- Жанр:
- Издательство:НИЦ Регулярная и хаотическая динамика
- Год:2000
- Город:Ижевск
- ISBN:5-93972-013-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Стивен Вайнберг - Первые три минуты краткое содержание
В книге крупнейшего американского физика-теоретика популярно и увлекательно рассказывается о современном взгляде на происхождение Вселенной. Описаны факты, подтверждающие модель «горячей Вселенной», рассказана история фундаментальных астрофизических открытий последних лет. С большим мастерством и научной точностью излагается эволюция Вселенной на ранних стадиях ее развития после «Большого взрыва».
В новое издание вошла также нобелевская лекция С. Вайнберга, в которой описывается история возникновения единой теории слабых и электромагнитных взаимодействий.
Для читателей, интересующихся проблемами космологии.
Первые три минуты - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
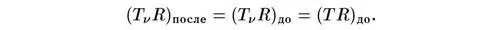
Отсюда заключаем, что после окончания процесса аннигиляции температура фотонов оказалась выше температуры нейтрино в
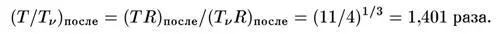
Нейтрино и антинейтрино, даже хотя они и не находятся в тепловом равновесии, дают важный вклад в космическую плотность энергии. Эффективное число разновидностей нейтрино и антинейтрино равно [61] Здесь учтены два сорта нейтрино ν e и ν μ и их античастицы. Вероятно, существует еще один сорт ν τ и ν - τ . — Прим. ред.
7/2, или 7/4 от эффективного числа разновидностей фотонов. (Имеются два спиновых состояния фотона.) В то же время четвертая степень температуры нейтрино меньше, чем четвертая степень температуры фотонов, на множитель (4/11) 4/3. Следовательно, отношение плотности энергии нейтрино и антинейтрино к плотности энергии фотонов
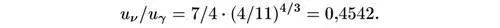
Закон Стефана-Больцмана (см. главу III) утверждает, что при температуре фотонов Т плотность энергии фотонов
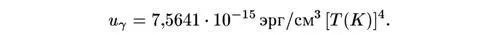
Следовательно, полная плотность энергии после электрон-позитронной аннигиляции равна
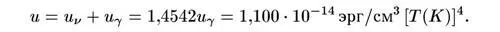
Мы можем перевести это в эквивалентную плотность массы, разделив на квадрат скорости света, и найдем тогда
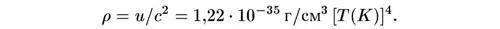
ДОПОЛНЕНИЯ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
ДОПОЛНЕНИЕ 1. КЛАССИЧЕСКАЯ
НЕРЕЛЯТИВИСТСКАЯ КОСМОЛОГИЯ
В предлагаемой книге Вайнберг для определения закона расширения Вселенной рассматривает шар, выделенный из безграничной среды. Гравитационное поле среды, окружающей шар, при этом не рассматривается: как известно, поле внутри сферически-симметричной оболочки равно нулю. Вывод Вайнберга правилен. Однако у читателя могут возникнуть сомнения, нет ли произвола в операции мысленного выделения шара [62] Если бы мы мысленно выделили эллипсоид вместо шара, то действительно результат оказался бы иным. Это обстоятельство можно считать проявлением так называемого гравитационного парадокса, т. е. трудности, возникающей при применении ньютоновой теории тяготения к безграничной среде с постоянной плотностью вещества.
. Поэтому полезно дать вывод, также основанный на ньютоновой теории тяготения, в котором искусственное выделение шара не используется. Логическая простота при этом покупается ценой некоторого математического усложнения решения. Приводимый ниже вывод оказывается также весьма полезным в теории образования галактик при рассмотрении возмущений идеального решения. Однако в этом дополнении мы не касаемся вопроса о возмущениях.
Итак, для определения закона расширения будем непосредственно рассматривать безграничную среду, ее гравитационный потенциал и движение.
Уравнение тяготения запишем в форме уравнения Пуассона:
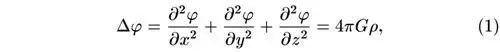
где φ — потенциал гравитационного поля; G — гравитационная постоянная; ρ — плотность. Будем искать сферически-симметричное решение с φ , зависящим только от r = (х 2+ у 2+ z 2) 1/2. Тогда
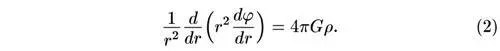
Решение этого уравнения имеет вид:
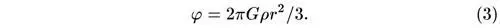
Мы привыкли к тому, что потенциал равен нулю на бесконечности; для ограниченной совокупности масс это так и есть. В безграничной Вселенной, равномерно заполненной веществом, это не так, однако нет никаких причин отказываться от приведенного решения.
Давление, так же как и плотность, считаем не зависящим от координат. В уравнение движения сплошной среды входит градиент давления, но в данном случае эта величина равна нулю.
Общий вид уравнения движения сплошной среды:
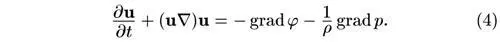
Подставим сюда выражение закона Хаббла
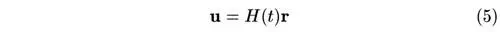
и используем выражение (3) для φ(r) и то, что grad ρ = 0. Сократив r , получим:
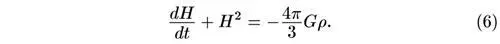
Наконец, составим уравнение неразрывности:
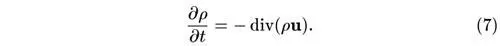
Подставив сюда хаббловское выражение скорости (5), найдем, что не зависящая от координат (но зависящая от времени) плотность удовлетворяет уравнению
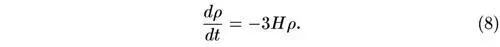
Система уравнений (6) и (8) полностью эквивалентна тем уравнениям, которые выписаны автором книги в дополнении 2. Для ее решения удобно поделить одно уравнение на другое. Тогда
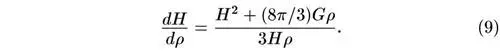
Это уравнение легко представить в виде линейного уравнения относительно величины H 2 :
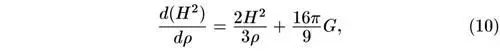
решение которого с заданными (измеренными в настоящее время) значениями Н 0 и ρ 0 нетрудно записать. Общее решение имеет вид ( А — константа интегрирования):
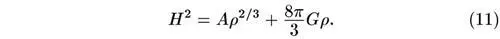
я2 = V/3 + YGp- (и)
Подставляя сегодняшние значения Н 0 и ρ 0 получаем окончательно
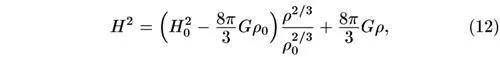
что полностью описывает и прошлое (при ρ > ρ 0 ) и будущее Вселенной. Еще одним интегрированием можно найти t(ρ) и тем самым связать Н и ρ с t .
Однако мы не останавливаемся на этом. Нашей целью была демонстрация того, что не нужно искусственно выделять какой-то шар, рассматривать находящуюся на краю точку, делать правдоподобные, но не строгие предположения о том, что внешняя (бесконечная!) область не влияет на движение.
Читать дальшеИнтервал:
Закладка:








![Стивен Вайнберг - Первые три минуты [litres]](/books/1068055/stiven-vajnberg-pervye-tri-minuty-litres.webp)

