Стивен Вайнберг - Первые три минуты

Постоянная Хаббла пропорциональна ρ 1/2 , и поэтому

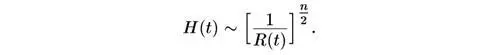
Но тогда скорость типичной галактики

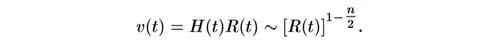
Элементарным результатом дифференциального исчисления является то, что если скорость пропорциональна какой-то степени расстояния, тогда промежуток времени, необходимый для того, чтобы попасть из одной точки в другую, пропорционален изменению отношения расстояния к скорости. Более точно, если ν пропорциональна R 1-n/2 , это соотношение имеет вид

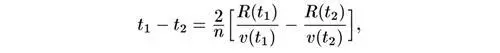
или

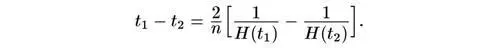
Можно выразить H(t) через ρ(t) , после чего получим

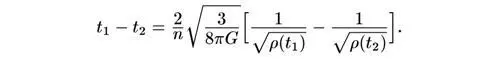
Таким образом, независимо от величины n пройденное время пропорционально изменению квадратного корня из обратной величины плотности.

Например, в течение всей эры преобладания излучения после аннигиляции электронов и позитронов плотность энергии равнялась

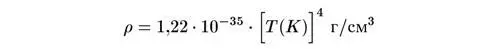
(см. мат. доп. 6). Кроме того, в этом случае n = 4. Таким образом, время, необходимое, чтобы Вселенная охладилась от 100 миллионов градусов до 10 миллионов градусов, составляет

Наш общий результат можно также выразить более просто, записав, что время, необходимое, чтобы плотность упала до значения ρ от некоторого значения, много большего, чем ρ , равно

(Если ρ(t 2) >> ρ(t 1) , мы можем пренебречь вторым членом в нашей формуле для t 1— t 2 ) Например, при температуре 3000 К плотность массы фотонов и нейтрино равнялась

ρ = 1,22 × 10 -35× 3000 4г/см 3= 9,9 × 10 -22г/см 3.

Это настолько меньше, чем плотность при температуре 10 8К (или 10 7К, или 10 6К), что время, требуемое на то, чтобы Вселенная охладилась от очень высоких температур на ранней стадии до 3000 К, можно рассчитать (полагая n = 4) просто как

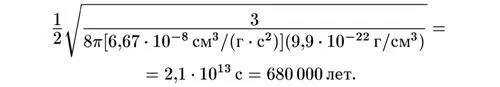
Мы показали, что время, необходимое, чтобы плотность Вселенной упала до значения ρ от значительно больших ранних значений, пропорционально 1/ ρ 1/2 , в то время как плотность ρ пропорциональна 1/ R n . Поэтому время пропорционально R n/2 или, другими словами,

Это остается справедливым до тех пор, пока кинетическая и потенциальная энергии не уменьшатся настолько, что станут сравнимы с их суммой — полной энергией.

Как отмечено в гл. II, в каждый момент времени t после начала имеется горизонт на расстоянии порядка ct , из-за которого никакая информация все еще не может нас достичь. Теперь мы видим, что при t → 0 R(t) уменьшается менее быстро, чем расстояние до горизонта, так что в достаточно ранние моменты времени любая данная «типичная» частица была за горизонтом.

Распределение Планка дает энергию du излучения черного тела в единице объема, приходящуюся на узкий интервал длин волн от λ до λ + dλ , в виде

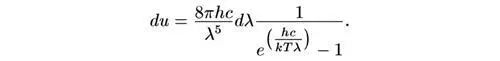
Здесь Т — температура; k = 1,38 × 10 -16эрг/К — постоянная Больцмана; с = 299 792 км/с — скорость света; е = 2,718… — числовая постоянная; h = 6,625 × 10 -27эрг·с — постоянная Планка, впервые введенная Максом Планком в качестве составной части этой формулы.

Для больших длин волн знаменатель в распределении Планка можно приближенно записать в виде

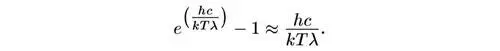
Следовательно, в этой области длин волн распределение Планка дает

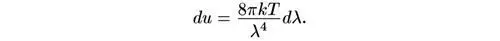
Это — формула Рэлея-Джинса . Если ее применить для произвольно малых длин волн, то du/dλ станет бесконечной при λ → 0 и полная плотность энергии излучения черного тела будет бесконечной.

К счастью, du в формуле Планка достигает максимума при длине волны

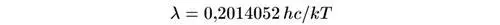
и затем плавно спадает с уменьшением длины волны. Полная плотность энергии излучения черного тела равна интегралу

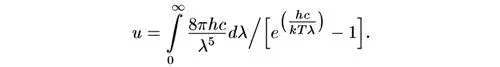
Подобные интегралы можно найти в стандартных таблицах определенных интегралов; в результате

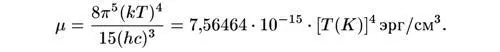
Это — закон Стефана-Больцмана .

Мы можем легко интерпретировать распределение Планка в терминах квантов света или фотонов. Каждый фотон имеет энергию, определяемую формулой

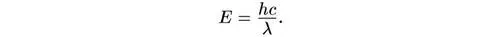
Отсюда, число фотонов dN в единице объема излучения черного тела, приходящееся на узкий интервал длин волн от λ до λ + dλ , равно

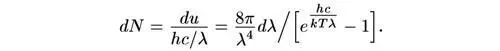
Полное число фотонов в единице объема 1 см 3равно тогда

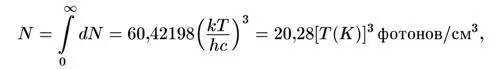
а средняя энергия фотона:

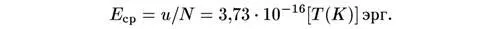
Рассмотрим теперь, что происходит с излучением черного тела в расширяющейся Вселенной. Предположим, что размер Вселенной изменился в f раз; например, если Вселенная удваивается в размере, то f = 2.

Как мы видели в главе II, длины волн изменяются пропорционально размеру Вселенной и будут иметь новое значение