Джеймс Глейк - Хаос. Создание новой науки

Вы спросите, каким маршрутом метод Ньютона приводит к корням квадратного уравнения на комплексной плоскости? Рассуждая геометрически, ответим, что метод позволяет отыскать тот из двух корней, который ближе к первоначальной догадке. Именно это Хаббард и объяснил своим студентам, когда однажды ему задали такой вопрос. «Уравнения, скажем, третьей степени решаются сложнее, — заметил преподаватель. — Я подумаю над этой проблемой, и мы займемся ею через неделю».

Он полагал, что наибольшую трудность для студентов будет представлять итерационный процесс, но никак не выдвижение начальной догадки. Но чем больше Хаббард размышлял на эту тему, тем менее определенным казалось то, что следует считать разумной догадкой или к чему на самом деле приводит метод Ньютона. Очевидным геометрическим решением было бы разделение плоскости на три равных сектора, похожих на куски пирога, в каждом из которых находилось бы по одному корню. Однако, как обнаружил Хаббард, идея не срабатывала: около границ секторов творились весьма странные вещи. Кроме того, выяснилось, что он далеко не первый специалист, споткнувшийся на этом чрезвычайно сложном вопросе. Так, Артур Кейли в 1879 г. попытался перейти от уравнений второй степени, которые казались вполне понятными, к пугающе сложным уравнениям третьей степени. Тем не менее Хаббард столетие спустя имел в своем распоряжении то, чего недоставало Кейли.

Хаббард относился к числу тех математиков, которые, уважая точность, презирали всяческие догадки, аппроксимации и эмпирику, основанную скорее на интуиции, чем на доказательстве. Даже спустя двадцать лет после появления в литературе упоминания об аттракторе Лоренца он продолжал настаивать на том, что фактически никто не знал , дали начало аттрактору уравнения Лоренца или нет. Это представлялось ему лишь недоказанным предположением, а уже знакомая нам двойная спираль, по его утверждению, была не доказательством, а простой очевидностью, тем, что изображают компьютеры.

Но сейчас, отринув сомнения, Хаббард все-таки обратился к компьютеру, чтобы выполнить то, что общепринятые методы обошли стороной. Компьютер не доказал бы ничего, но, по крайней мере, он мог бы кое-что прояснить, чтобы математик понял, что именно ему предстоит доказать. Итак, Хаббард начал экспериментировать, рассматривая Ньютонов метод не как средство решения задач, а как саму задачу. Он взял в качестве примера простое кубическое уравнение x ³ — 1 = 0, при решении которого требуется найти кубический корень из единицы. В случае с действительными числами решение вполне тривиально — единица. Однако данный многочлен имеет также два комплексных корня:

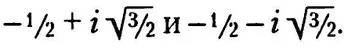
Нанесенные на комплексную плоскость, три указанных корня образуют равносторонний треугольник, одна вершина которого будет находиться на трех часах, другая — на семи часах, и третья — на одиннадцати часах. Коль скоро в качестве начальной точки выбрано любое комплексное число, вопрос заключается в том, чтобы увидеть, какое именно из трех решений даст вычисление по методу Ньютона. Это все равно что рассматривать данный метод как динамическую систему, а три решения — как три аттрактора. Или представить комплексную плоскость в виде ровной поверхности, спускающейся к трем углублениям. Мраморный шарик, начав катиться с любой точки на плоскости, приведет в одну из долин. Какую?

Хаббард приступил к рассмотрению бесконечного числа точек, составляющих плоскость. Его компьютер переходил от точки к точке, рассчитывая Ньютоновым методом каждую из них и кодируя результат определенным цветом. Те начальные точки, которые вели к первому решению, стали синими, точки, генерировавшие второе решение, — красными, а тем, которые давали третий результат, был присвоен зеленый цвет. Математик заметил, что даже при самом грубом приближении плоскость в силу динамики метода действительно делится на три сектора. Как правило, точки, близкие к определенному решению, быстро вели прямо к нему. Тем не менее систематическое компьютерное исследование выявило сложную скрытую организацию, которая ранее никогда не могла быть обнаружена математиками, способными только рассчитывать точки в разных зонах. В то время как некоторые начальные предположения быстро приводили к одному из корней, другие словно бы «прыгали» рядом с ним совершенно произвольно, пока не приближались наконец к решению. Иногда казалось, что точка может стать началом периодического цикла, который будет повторяться вечно, не достигая ни одного из трех возможных корней.

Когда Хаббард запустил компьютер, намереваясь более детально исследовать пространство, начала вырисовываться картина, которая сбила с толку и преподавателя, и его студентов. Например, вместо аккуратного «гребня» между синей и красной долинами математик увидел пятна зеленого цвета, соединенные словно бусины ожерелья. Это выглядело так, словно шарик, попавший в ловушку на стыке двух соседних долин, остановился в третьей, самой отдаленной зоне. Граница между двумя цветами никогда полностью не формировалась, и даже при увеличении линия между зеленым пятном и синей областью включала в себя клочки красного цвета. И так снова и снова… Линия границы в конце концов открыла Хаббарду особое свойство, которое показалось бы весьма странным даже человеку, знакомому с жуткими фракталами Мандельбро: ни одна из точек не разделяет только два цвета. Где бы два цвета ни старались соединиться, там всегда появляется третий, внедряясь новыми, внутренне подобными рядами. Непостижимо, но каждую пограничную точку окаймляли зоны всех трех цветов.

Хаббард начал изучать обнаруженные сложные формы. В результате его работа, а также исследования коллег ознаменовали собой новый штурм проблемы динамических систем. Ученому стало ясно, что схематичное отображение Ньютонова метода — одно из целого семейства еще не открытых изображений, передающих действия сил в реальном мире. Майкл Барнсли столкнулся с другими фрагментами такого же рода, а Бенуа Мандельбро, как вскоре поняли и Хаббард и Барнсли, обнаружил прототип всех этих форм.

Множество Мандельбро, как любят повторять его почитатели, является наиболее сложным объектом во всей математике. Чтобы увидеть его полностью — круги, усыпанные колючими шипами, спирали и нити, завивающиеся наружу и кругом, с выпуклыми пестрыми молекулами, висящими, словно виноградины на личной лозе Господа Бога, — не хватит целой вечности. Если разглядывать модель в цвете на подходящем экране, множество Мандельбро кажется более фрактальным, нежели сами фракталы, настолько оно изобилует сложностью, пронизывающей все масштабы картины. Построение каталога различных составляющих элементов или числовое изображение очертаний системы потребует бесконечного количества данных. Однако, как это ни парадоксально, для передачи полного описания системы по линии связи хватит нескольких десятков кодовых символов, а в компьютерной программе содержится достаточно информации, чтобы воспроизвести систему целиком. Догадавшиеся первыми, каким образом в системе смешиваются сложность и простота, были застигнуты врасплох — даже сам Мандельбро. Система превратилась в эмблему хаоса для широкой публики. Она замелькала на глянцевых обложках тезисов конференций и инженерных журналов и сделалась украшением выставки компьютерного искусства, показанной во многих странах в 1985–1986 годах. Ее красота ощущалась сразу. Гораздо труднее было уловить математический смысл. Ученые долго вникали в ее суть.