Джеймс Глейк - Хаос. Создание новой науки
- Название:Хаос. Создание новой науки
- Автор:
- Жанр:
- Издательство:Амфора
- Год:2001
- Город:Санкт-Петербург
- ISBN:5-94278-139-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Джеймс Глейк - Хаос. Создание новой науки краткое содержание
В 1970-х годах ученые начинают изучать хаотические проявления в окружающем нас мире: формирование облаков, турбулентность в морских течениях, колебания численности популяций растений и животных… Исследователи ищут связи между различными картинами беспорядочного в природе.
Десять лет спустя понятие «хаос» дало название стремительно расширяющейся дисциплине, которая перевернула всю современную науку. Возник особый язык, появились новые понятия: фрактал, бифуркация, аттрактор…
История науки о хаосе — не только история новых теорий и неожиданных открытий, но и история запоздалого постижения забытых истин. Эта книга — яркое и образное повествование о сложных и глубоких вещах, окрашенное драматизмом и поэтичностью. Прочитав «Хаос», вы уже никогда не будете смотреть на мир прежними глазами.
Хаос. Создание новой науки - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Неисчислимое разнообразие фрактальных форм может быть образовано итерацией в комплексной плоскости, но система Мандельбро была одной-единственной. Смутная и призрачная, она начала вырисовываться, когда ученый попытался найти способ сведения к общим законам класса форм, известного как множества Джулиа. Множества эти были открыты и изучены еще во время Первой мировой войны французскими математиками Гастоном Джулиа и Пьером Фато, работавшими без каких бы то ни было компьютерных изображений. Мандельбро в двадцатилетнем возрасте познакомился с их скромными рисунками и прочитал их работу, уже канувшую в безвестность. Именно множества Джулиа во всем разнообразии обличий оказались тем, что поставило в тупик Барнсли. Некоторые из порождаемых ими форм похожи на круги, проколотые и деформированные во многих местах, что придает им фрактальную структуру, другие разбиты на зоны, третьи — на разъединенные пылинки. Для их описания не подходят ни обычные слова, ни понятия Евклидовой геометрии. Французский математик Адриен Доуди заметил: «Получив непредсказуемо многоликие образы множеств Джулиа, замечаем, что некоторые выглядят словно пухлое облако, другие представляют собой тощий куст ежевики, третьи похожи на искорки, плывущие в воздухе после фейерверка. Один объект напоминает кролика, и многие имеют хвосты, как у морских коньков».
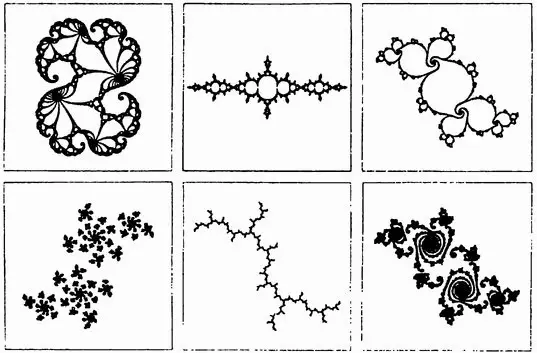
Рис. 8.1. Примеры изображений, полученных с помощью множеств Джулиа.
В 1979 г. Мандельбро обнаружил, что может создать в пределах комплексной плоскости один образ, который послужит своего рода каталогом множеств Джулиа, ориентиром для каждого из составляющих эти множества объектов. Тогда он изучал итерационные решения квадратных и тригонометрических уравнений (последние включали функции синуса и косинуса). Даже основываясь на гипотезе о порождении простотой сложности, он отнюдь не сразу понял, насколько необычным являлся объект, возникший на экране монитора в его кабинете в Гарварде. Программисты, пытаясь эффективно распределить память компьютеров, корпели над новыми интерполяциями точек в машине IBM с обладающим низким разрешением, черно-белым дисплеем, а ученый торопил их, желая рассмотреть мельчайшие детали. Вдобавок приходилось следить за тем, чтобы не попасть в ловушку артефактов, возникающих из-за сбоя в машине и исчезающих при изменении программы.
Мандельбро обратился к простейшим изображениям, запрограммировать которые не составляло труда. На грубо набросанной координатной сетке, где несколько раз повторялась петля обратной связи, возникли первые контуры кругов или дисков. Проделанные вручную расчеты показали, что с математической точки зрения они вполне реальны и не являются некими вычислительными странностями. Справа и слева от главных дисков появлялись иные неясные очертания. Как позже вспоминал сам Мандельбро, воображение нарисовало ему нечто большее — целую иерархию форм, где от атомов, словно ростки, отпочковываются всё новые и новые атомы, и так до бесконечности. А там, где система пересекала действительную ось, ее уменьшающиеся с каждым разом диски подчинялись определенному масштабированию с геометрической регулярностью, которую ученые, занимающиеся динамическими системами, определяют сейчас как последовательность бифуркаций Файгенбаума.
Эти исследования подтолкнули Мандельбро к продолжению работы и совершенствованию первых черновых изображений. Вскоре он обнаружил некие включения, собиравшиеся по краям дисков и «плававшие» в близлежащем пространстве. Продолжая рассчитывать мельчайшие детали, он вдруг почувствовал, что удача покинула его, — на картинах вместо четких изображений появлялась путаница. Тогда он направился обратно в исследовательский центр IBM, надеясь попытать удачи на компьютерах корпорации в частном порядке, чего не мог позволить себе в Гарварде. К удивлению Мандельбро, нарастание путаницы в изображениях говорило о чем-то реальном. Отростки и завитки медленно отделились от основного островка, и возникла кажущаяся однородной граница, которая распадалась на цепочку спиралей, напоминавших хвосты морского конька. Иррациональное породило нечто рациональное.
Система Мандельбро являет собой скопление точек, и каждая точка комплексной плоскости — иными словами, каждое комплексное число — или входит в их множество, или находится вне его пределов. Определить границы множества можно одним способом — тестированием каждой точки с помощью простого итерационного процесса. Для этого необходимо, выбрав комплексное число, возвести его в квадрат, прибавить результат к первоначальному числу, итог вновь возвести в квадрат, вновь прибавить результат к первоначальному числу, вновь возвести итог в квадрат и так далее, снова и снова. Если полученное число стремится к бесконечности, значит, точка не входит в систему Мандельбро. Если же итог имеет предел (может быть «пойман» какой-нибудь из повторяющихся петель или хаотично блуждать), в таком случае точка находится в пределах системы.
Повторение процедуры неопределенное число раз и постоянная проверка того, бесконечен ли ее результат, напоминает процессы обратной связи в повседневной жизни. Представьте себе, что в аудитории вы размещаете микрофон, усилители и громкоговорители. Вас беспокоит, не возникнут ли пронзительные завывания при обратной связи. Что это такое? Если микрофон достаточно чувствителен, усиленный громкоговорителем звук достигнет его и породит бесконечные, еще более громкие отклики. С другой стороны, если звуки слабы, они просто затухнут. Чтобы построить модель процесса обратной связи, необходимо выбрать начальное число, умножить его на самое себя, затем вновь умножить получившееся число на самое себя и т. д. Мы обнаружим, что большие числа быстро приведут к бесконечности: 10, 100, 10 000… Маленькие же числа стремятся к нулю: ½, ¼, 1/ 16… Чтобы построить геометрическое изображение, мы определим совокупность численных значений, при подстановке которых данное уравнение не стремится к бесконечности. Примем во внимание точки на прямой от нуля и далее. Если точка ведет к эффекту обратной связи (визгу в микрофоне), закрасим ее белым цветом, а все другие — черным. Вскоре у нас появится изображение в виде линии, черной от нуля до единицы.
При исследовании одномерного процесса нет необходимости прибегать к эксперименту. Достаточно просто установить, что числа, которые больше 1, ведут к бесконечности, чего нельзя сказать о всех остальных. Но для изучения формы в двух измерениях комплексной плоскости с помощью процесса итерации знать уравнение, как правило, недостаточно. В отличие от традиционных геометрических форм, таких как окружности, эллипсы и параболы, система Мандельбро не допускает никаких сокращенных вариантов. Определить, какая форма подходит к каждому конкретному уравнению, удается только методом проб и ошибок. Именно он привел исследователей к неизведанным землям, скорее путем Магеллана, чем дорогой Евклида.
Читать дальшеИнтервал:
Закладка:









