О. ОРЕ - Приглашение в теорию чисел

Магический квадрат Б. Франклина перед вами (рис. 11) и вы можете сами проверить его замечательные свойства.

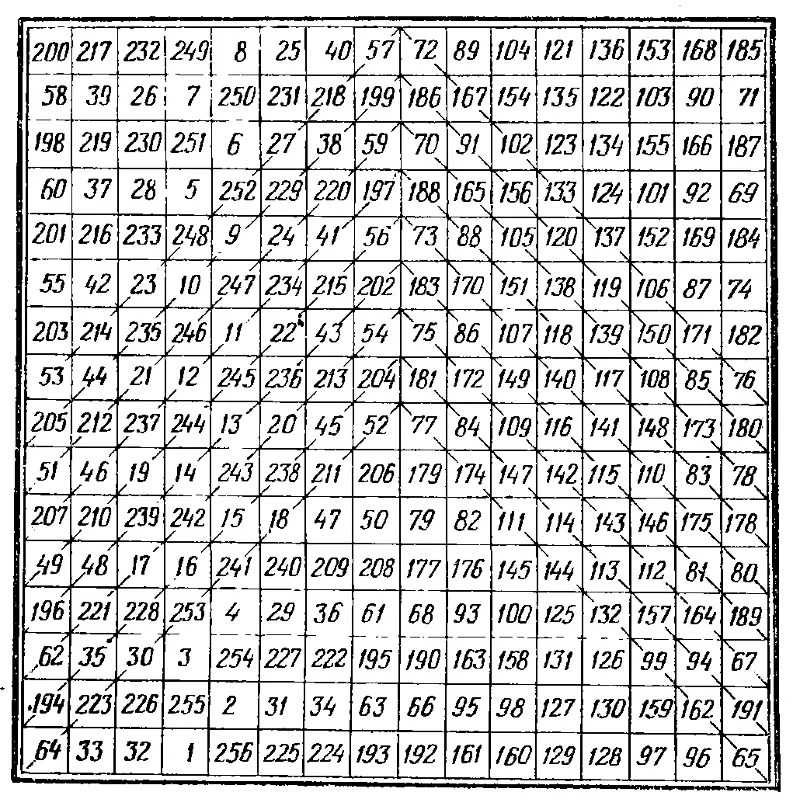
Рис. 11.

Б. Франклин по праву гордился своим творением, что видно из продолжения его письма: «На следующее утро я послал этот квадрат нашему другу, который через несколько дней вернул его в ответном письме со следующими словами: „Я возвращаю тебе твой удивительный, а может быть, самый изумительный магический квадрат, в котором…", но этот комплимент слишком экстравагантен, и поэтому ради него, а также ради самого себя, мне не следует его повторять. К тому же это и необязательно, так как я не сомневаюсь, что вы охотно согласитесь, что этот квадрат 16 × 16 является самым магически-магическим из всех магических квадратов, составленных когда-либо каким-либо магом». Более подробные сведения о построении магических квадратов можно найти в книгах: Е. Я. Гуревич. Тайна древнего талисмана. — М.: Наука, 1969 и И. М. Постников. Магические квадраты. — М.: Наука, 1964.

Система задач 1.5.

1. Мог ли Дюрер использовать вместо своего квадрата, изображенного на рис. 9, какие-либо другие квадраты, в которых тот же год фигурировал таким же образом?

2. Дюрер прожил до 1528 г. Смог ли бы он датировать какую-нибудь из своих более поздних картин таким же способом?

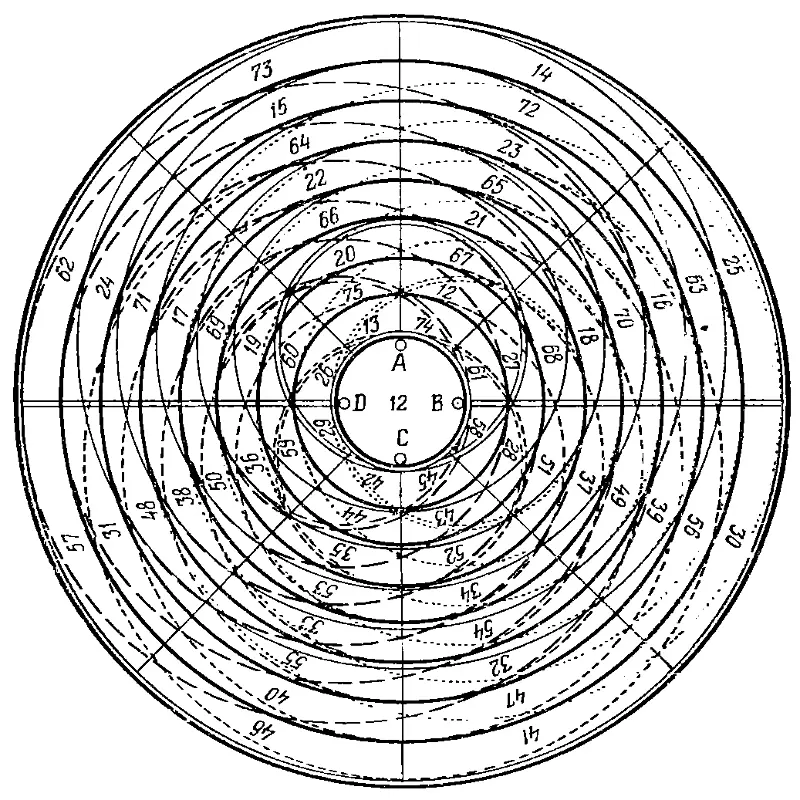
Рис. 12. Репродукция магического круга Франклина. Оригинал, выполненный в цвете, был продан частному коллекционеру на аукционе в Нью-Йорке.

3. Изучите некоторые свойства магического круга Б. Франклина (рис. 12).

Должно быть, одним из первых свойств чисел, открытых человеком, было то, что некоторые из них могут быть разложены на два или более множителя, например,

6 = 2 • 3, 9 = 3 • 3, 30 = 2 • 15 = 3 • 10,

в то время как другие, например,

3, 7, 13, 37,

не могут быть разложены на множители подобным образом. Давайте вспомним, что вообще, когда число

c = a b (2.1.1)

является произведением двух чисел a и b , то мы называем а и b множителями или делителями числа с . Каждое число имеет тривиальное разложение на множители

с = 1 • с = с • 1. (2.1.2)

Соответственно мы называем числа 1 и с тривиальными делителями числа с .

Любое число с > 1, у которого существует нетривиальное разложение на множители, называется составным . Если число с имеет только тривиальное разложение на множители (2.1.2), то оно называется простым . Среди первых 100 чисел простыми являются следующие 25 чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Все остальные числа, кроме 1, являются составными. Мы можем сформулировать следующее утверждение:

Теорема 2.1.1.Любое целое число с> 1 является, либо простым, либо имеет простой множитель.

Доказательство. Если с не является простым, числом, то у него есть наименьший нетривиальный множитель р . Тогда р — простое число, так как если бы р — было составным, то число с имело бы ещё меньший множитель.

Теперь мы подошли к нашей первой важной задаче в теории чисел: как определить, является ли произвольное число простым или нет, и в случае, если оно составное, то как найти какой-либо его нетривиальный делитель?

Первое, что может прийти в голову, — это попытаться разделить данное число с на все числа, меньшие его. Но надо признать, что этот способ мало удовлетворителен. Согласно теореме 2.1.1 достаточно делить на все простые числа, меньшие √ с . Но мы можем значительно упростить задачу, заметив, что при разложении на множители (2.1.1) оба множителя а и b не могут быть больше, чем c , так как в противном случае мы получили бы

ab > √ с • √ с ,

что невозможно. Таким образом, чтобы узнать, имеет ли число с делитель, достаточно проверить, делится ли число с на простые числа, не превосходящие — √ с.

Пример 1. Если с = 91, то √ с = 9….; проверив простые числа 2, 3, 5, 7, находим, что 91 =7 13.

Пример 2. Если с =1973, то находим, что √ с = 44…. Так как ни одно из простых чисел до 43 не делит с , то это число является простым.

Очевидно, что для больших чисел этот метод может быть очень трудоемким. Однако здесь, как и при многих других вычислениях в теории чисел, можно использовать современные методы. Довольно просто запрограммировать на ЭВМ деление данного числа с на все целые числа до √ с и печатание тех из них, которые не имеют остатка, т. е. тех, которые делят с .

Другим очень простым методом является применение таблиц простых чисел, т. е. использование простых чисел уже найденных другими. За последние 200 лет было составлено и издано много таблиц простых чисел. Наиболее обширной из них является таблица Д. X. Лемера, содержащая все простые числа до 10 000 000. Наша таблица 1 содержит все простые числа до 1000.

Таблица 1

Простые числа среди первой тысячи чисел

Некоторые энтузиасты-вычислители уже подготовили таблицы простых чисел, превосходящих 10 000 000. Но, по-видимому, не имеет большого смысла идти на значительные затраты и усилия, чтобы опубликовать эти таблицы. Лишь в очень редких случаях математику, даже специалисту в теории чисел, приходится решать вопрос о том, является ли какое-то большое число простым. Кроме того, большие числа, о которых математик хочет узнать, являются они составными или простыми, не берутся им произвольно. Числа, которые он хочет исследовать, обычно появляются в специальных математических задачах, и, таким образом, эти числа имеют очень специфическую форму.

Система задач 2.1.

1. Какие из следующих чисел являются простыми: а) год вашего рождения; б) текущий год; в) номер вашего дома.

2. Найдите простое число, следующее за простым числом 1973.

3. Заметим, что числа от 90 до 96 включительно являются семью последовательными составными числами; найдите девять последовательных составных чисел.

В течение нескольких столетий шла погоня за простыми числами. Многие математики боролись за честь стать открывателем самого большого из известных простых чисел. Разумеется, можно было бы выбрать несколько очень больших чисел, не имеющих таких очевидных делителей, как 2, 3, 5, 7, и проверить, являются ли они простыми числами. Этот способ, как мы вскоре убедимся, не очень эффективен. Теперь эта погоня утихла, она идет только в одном направлении, оказавшемся удачным.