О. ОРЕ - Приглашение в теорию чисел

Простые числа Мерсенна являются простыми числами специального вида

М р = 2 p- 1, (2.2.1)

где р — другое простое число. Эти числа вошли в математику давно, они появляются еще в евклидовых размышлениях о совершенных числах, которые мы рассмотрим позже. Свое название они получили в честь французского монаха Мерена Мерсенна (1588–1648), который много занимался проблемой совершенных чисел.

Если начать вычислять числа (2.2.1) для различных простых чисел р , то видно, что не все они оказываются простыми. Например,

М 2= 2 2— 1 = 3 = простое,

М 3 = 2 3— 1 = 7 = простое,

М 5= 2 5— 1 = 31 = простое,

М 7= 2 7— 1 = 127 = простое,

М 11= 2 11— 1 = 2047 = 23 89.

Общий способ нахождения больших простых чисел Мерсенна состоит в проверке всех чисел М p для различных простых чисел р .

Эти числа очень быстро увеличиваются и столь же быстро увеличиваются затраты труда на их нахождение. То, что с этой работой все-таки можно справиться уже для довольно больших чисел, объясняется существованием эффективных способов выяснения простоты для чисел такого вида.

В исследовании чисел Мерсенна можно выделить раннюю стадию, достигшую своей кульминации в 1750 году, когда Леонард Эйлер [5] Леонард Эйлер (1707–1783) — выдающийся математик, родившийся в Швейцарии, большую часть жизни провел в России, являясь членом Петербургской Академии наук. ( Прим. перев. ) установил, что число М 31является простым. К этому времени было найдено восемь простых чисел Мерсенна, соответствующих значениям

р = 2, р = 3, р = 5, р = 7, р = 13, р = 17, p = 19, р = 31.

Эйлерово число M 31оставалось самым большим из известных простых чисел более ста лет. В 1876 году французский математик Лукас установил, что огромное число

М 127 = 170141183460469231731687303715884105727

является простым числом. Ну и число! С 39 цифрами. Простые числа Мерсенна, меньшие этого числа, задаются значениями р , указанными выше, а также значениями

р = 61, р = 89, р = 107.

Эти 12 простых чисел Мерсенна были вычислены с помощью только карандаша и бумаги, а для вычисления следующих уже использовались механические настольные счетные машины. Появление вычислительных машин с электрическим приводом позволило продолжить поиски, доведя их до р = 257. Однако результаты были неутешительными, среди них не оказалось новых простых чисел Мерсенна.

Затем задача была переложена на плечи ЭВМ. Создание все более высокопроизводительных ЭВМ дало возможность продолжить поиск новых простых чисел Мерсенна. Д. X. Лемер установил, что значения

р = 521, р = 607, р = 1279, р = 2203, р = 2281

дают простые числа Мерсенна. Дальнейшие поиски также увенчались успехом. Ризель (1958) показал, что

р = 3217,

дает простое число Мерсенна, а Гурвиц (1962) нашёл еще два таких значения:

р = 4253, р = 4423.

Огромного успеха добился Гиллельс (1964), который нашел простые числа Мерсенна, соответствующие значениям

р = 9689, р = 9941, р = 11213.

Итак, общий урожай составил 23 простых числа Мерсенна, и, так как мощности ЭВМ продолжают увеличиваться, мы надеемся на дальнейший успех. Простое число Лукаса М 127, как мы уже упоминали, имеет 39 цифр. Даже вычисление самого большого из известных простых чисел, числа M 11213, является довольно сложной задачей и, по-видимому, нет смысла воспроизводить здесь это число. Если же мы захотим узнать, сколько цифр содержит это число, то мы можем сделать это, не вычисляя самого числа.

Вместо нахождения количества цифр числа М р = 2 p — 1 рассмотрим эту задачу для числа М р + 1 = 2 р.

Эти два числа имеют одинаковое количество цифр, так как если бы число М р + 1 имело на одну цифру больше, то оно должно было бы оканчиваться на 0. Но это невозможно ни для какой степени числа 2, что видно из ряда

2, 4, 8, 16, 32, 64, 128, 266….

в котором последняя цифра в каждом числе может быть только одним из чисел

2, 4, 8, 6.

Чтобы найти количество цифр числа 2 p , вспомним, что Ig 2 p = p lg 2. Из таблиц находим, что Ig 2 приближенно равняется 0,30103, откуда

lg 2 p = p lg 2 = р • 0,30103.

Для р = 11213 получаем

lg 2 11213= 3375,449…,

и так как характеристика этого числа равна 3375, то мы приходим к выводу, что число 2 pимеет 3376 цифр.

Итак, мы можем сказать следующее.

Самое большое известное в настоящее время простое число имеет 3376 цифр. (Здесь слова «в настоящее время» имеют существенное значение.) Это число было найдено на ЭВМ Иллинойского университета (США). Математический факультет этого университета был так горд своим достижением, что изобразил это число на своем почтовом штемпеле, таким образом воспроизводя его на каждом отсылаемом письме, для всеобщего восхищения.

Существует также еще один тип простых чисел с большой и интересной историей. Они были впервые введены французским юристом Пьером Ферма (1601–1665), который прославился своими выдающимися математическими работами. Первыми пятью простыми числами Ферма являются

F 0= 2 2 °+ 1 = 3,

F 1= 2 2¹+ 1 = 5,

F 2= 2 2²+ 1 = 17,

F 3= 2 2³+ 1 = 257,

F 4= 2 2ˆ 4 + 1 = 65 537.

В соответствии с этой последовательностью общая формула для простых чисел Ферма должна иметь вид

F n = 2 2ⁿ+1. (2.3.1)

Ферма был абсолютно уверен, что все числа этого вида являются простыми, хотя он не проводил вычислений других чисел, кроме указанных пяти. Однако это предположение было сдано в архив неоправдавшихся математических гипотез после того, как Леонард Эйлер сделал еще один шаг и показал, что следующее число Ферма

F 5= 4 294 967 297 = 641 6 700 417

не является простым, что и показывает приведенная запись. Возможно, что этим история чисел Ферма была бы закончена, если бы числа Ферма не появились в совсем другой задаче, задаче построения правильных многоугольников при помощи циркуля и линейки.

Правильным многоугольником называется многоугольник, вершины которого лежат на некоторой окружности на одинаковых расстояниях друг от друга (рис. 13). Если у правильного многоугольника n вершин, то мы называем его правильным n-угольником .

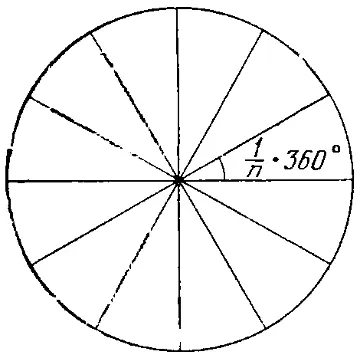
Рис 13.

Если мы проведем n радиусов, соединяющих центр окружности с вершинами, то получим n центральных углов величиной

1/ n 360°

каждый. Если можно построить угол, имеющий эту величину, то можно построить и этот n -угольник.

Древние греки очень хотели найти методы построения правильных многоугольников с помощью циркуля и линейки. Разумеется, они умели строить простейшие из них — равносторонний треугольник и квадрат. С помощью повторного деления пополам центрального угла они могли также построить правильные многоугольники с