Вернер Гильде - Зеркальный мир

Построение эллипса с помощью нитки

Датский астроном Тихо Браге (1546-1601) с неутомимым прилежанием измерял астрономические величины без телескопа. Вначале он работал у себя на родине, а позднее стал придворным астрономом и астрологом германского императора Рудольфа II в Праге. После смерти Тихо Браге на эту должность был приглашен Иоганн Кеплер (1571-1630), который приступил к своим расчетам движения планет на основе рядов измерений, выполненных Браге. Дело подвигалось очень успешно: результаты вычислений лишь на 10' отклонялись от действительной картины ночного неба. Попробуйте ясным вечером, когда появляются первые звезды, измерить на небе расстояние в 10 или 20' с помощью руки (см. раздел «Что такое подобие?»). Вы сразу поймете, что разницу в 10' почти или совсем невозможно заметить. Конечно, Тихо Браге пользовался в своих измерениях не большим пальцем, а специальным прибором - квадрантом.

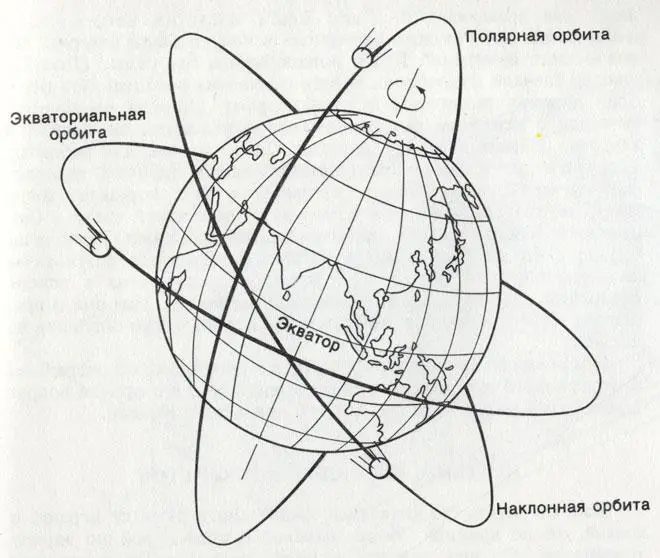
Большинство искусственных спутников облетает Землю по эллиптическим орбитам

Кеплер неоднократно повторял расчеты, но никак не мог объяснить себе эту ничтожную ошибку. В конце концов остались лишь две возможности. Либо Браге допустил неточность в измерениях, либо модель Коперника в чем-то была неверна. На повторение измерений Браге понадобились бы годы. Поэтому Кеплер сначала попробовал внести изменения в модель. Он перебрал дюжину различных круговых орбит. Ошибка не исчезла. И тогда с глубоким внутренним сопротивлением он принял в качестве планетных орбит эллипсы. Сама мысль, что небесные тела могут двигаться по столь несовершенным орбитам, казалась ему святотатством. Кеплер, несомненно, был поражен, когда после некоторых колебаний измерения Браге вдруг сразу и безошибочно совпали с его эллиптическими орбитами. Приблизительно в то же время, когда Кеплер опубликовал результаты своих вычислений, книга Коперника была включена в список сочинений, запрещенных католической церковью. Там она и пребывала в течение 200 лет, до 1820 г. Но это не могло повлиять на истину!

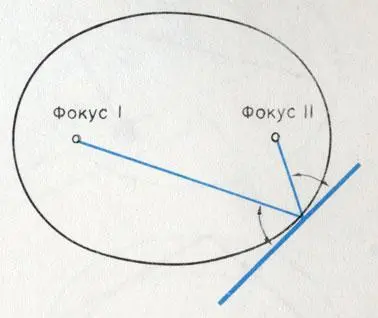
Кратчайшее расстояние от первого фокуса до любой точки на кривой эллипса и от нее до второго фокуса всегда удовлетворяет закону отражения от касательной в этой точке

Когда мы слышим сегодня по радио сообщение об очередном запуске нового спутника, стоит вспомнить, что его орбита вокруг Земли будет эллиптической, как это предсказал Кеплер.

КРАТКИЙ КУРС ДЛЯ ХОККЕИСТОВ

Если большинство читателей нашей книги сами не играют в хоккей, то по крайней мере знакомы с этой игрой по экрану телевизора. Пятеро крепких парней, защищенных толстыми бандажами и шлемами, пытаются загнать маленький диск, называемый шайбой, в ворота противника, в чем им столь же энергично стараются помешать пятеро других не менее крепких парней. Так вот, хоккей на льду отличается от большинства подобных игр с мячом одним существенным моментом: в нем не бывает аутов.

Когда в футболе, теннисе или в другой аналогичной игре мяч покидает пределы игрового поля, игра останавливается, мяч возвращают назад и один из игроков, соблюдая известные правила, снова вводит его в игру. На льду дело обстоит иначе. Поле обрамлено бортиком, прочным деревянным барьером, который отбрасывает ударившуюся о него шайбу обратно, и игра продолжается без всякого перерыва. Хоккеисты бессознательно овладевают законами отражения. Они используют правило «угол падения равен углу отражения», чтобы обыграть противника. Пока шайба ударяется о прямолинейные участки бортика, все происходит очень просто. Но совсем иная ситуация складывается в углах поля. Там бортик имеет криволинейную форму. Когда шайба отскакивает от него в таких местах, то летит, скользя по льду, в самых неожиданных направлениях. Если вы не интересуетесь хоккеем, все равно прочтите этот раздел. То, что справедливо для углов ледяной спортплощадки, справедливо и для зеркал для бритья, зеркальных рефлекторов в карманных фонариках, громкоговорителей. Во многих семьях имеются малоформатные игры для испытания ловкости. Суть их в том, чтобы загнать в луночки поля, заключенного под стеклом, один или несколько шариков. Шарики наталкиваются на стенку игрового поля, обычно имеющего округлую форму. Куда же они отскочат?

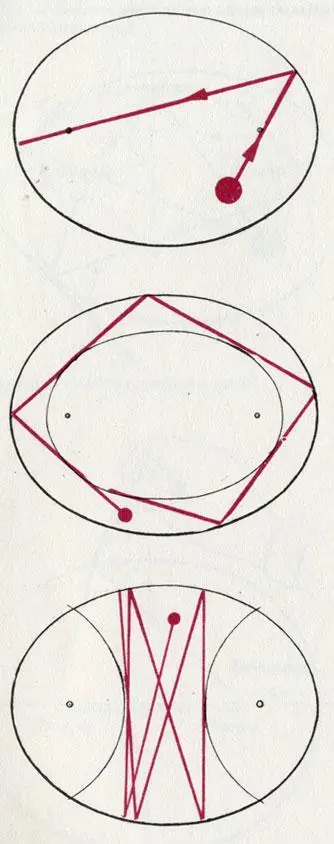
Возможные случаи отражения в эллипсе. На практике они используются при строительстве волнорезов и конструировании неразбрызгивающих воронок (хоботов), например при бетонировании и в литейном деле

Большинству из нас еще со школьной скамьи знакомо понятие конических сечений. Если разрезать конус перпендикулярно его главной оси, то получится круг, а если разрез сделать косо, круг превратится в эллипс. Чем больший наклон имеет сечение, тем более вытянутым (более эксцентрическим) становится эллипс. Наконец, если плоскость сечения ориентирована параллельно образующей конуса, то эллипс переходит в параболу. А если построить зеркальное отражение конуса так, чтобы оно и сам конус соприкасались вершинами, и потом провести сечение, проходящее через оба конуса, то возникает гипербола.

Следовательно, у Коперника и у Кеплера не было, в сущности, никаких оснований для особого пристрастия к той или иной форме планетных орбит. В конце концов, круг - это только частный случай эллипса. Строго говоря, нам достаточно знать из курса математики лишь уравнения эллипса. Круг также охватывается ими. Центр круга расщепляется на два фокуса эллипса. Или, выражаясь иначе, оба фокуса эллипса в круге совпадают между собой и называются его центром.

Иоганн Кеплер установил, что Солнце расположено в одном из фокусов эллиптической орбиты Земли. В свою очередь Земля находится в одном из фокусов эллиптических орбит многих искусственных спутников, вращающихся вокруг нее. В обоих случаях в другом фокусе нет ничего. Тем самым вся система становится резко асимметричной. Мы, однако, можем утешиться тем, что зеркальное отражение эллипса столь же устойчиво. Поэтому при запуске спутника у нас всегда есть две возможности для образования эллиптических орбит, между которыми мы можем выбирать.

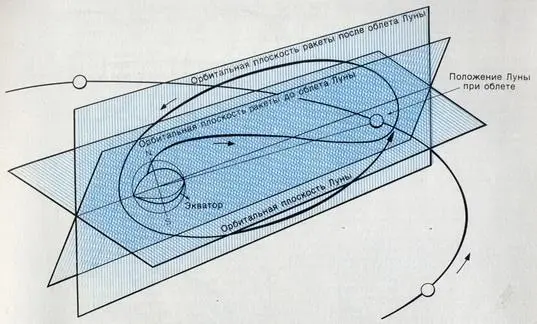
В то время как ракета отражается гравитационным полем планеты, сама планета перемещается и сообщает ракете дополнительный импульс