Надежда Ефремова - Тестовый контроль в образовании

Поисками таких моделей занимались многие зарубежные математики, среди которых особо следует отметить работы Д. Батесона и других (D. Bateson, C. Nikol, T. Achroeder) [228], Р. Берка (R. Berk) [229], А. Бинета и Т. Симона (A. Binet and T. Simon) [230], А. Бирнбаума (A. Birnbaum) [231], Б. Блума (B. Bloom) [232], Я. Кевиса (J. Keeves) [238], К. Лорда (K. Lord) [241 —244], Г. Раша (G. Rasch) [247 —249], Д. Вайса и Г. Кинсбери (D.J. Weiss, G.G. Kingsbury) [252]. Применение этих моделей в отечественной практике тестирования изложено в работах В.С. Аванесова [1], М.Б.Челышковой [195—200], Ю.М.Неймана и В.А.Хлебникова [134], других авторов.

Использование специальных моделей измерения, соединяющих латентные параметры испытуемых с наблюдаемыми результатами выполнения теста, позволяет устранить многие трудности. В рамках IRT оценки качества подготовленности испытуемых можно отождествлять с модифицированными результатами тестовых измерений. При этом, казалось бы, совсем разные понятия «качество» и «количество» не противопоставляются друг другу, а, по определению М.Б. Челышковой и Г.С. Ковалевой, «вкладываются один в другой как показатели интенсивности проявления качества» [199]. Это позволяет представить образовательный процесс в качественных показателях и своевременно корректировать его.

Для решения задач педагогического измерения плодотворным явилось определение знания как объективно и субъективно достаточного признака истинности или проявления логического суждения. При этом латентно–структурный анализ нацелен на выявление внутренних, скрытых качеств и факторов поведения (деятельности) испытуемого посредством математических моделей измерения и статистической обработки полученных результатов. IRT представляет некоторое структурное построение или математическую модель, позволяющую соединить между собой несколько латентных переменных. В соответствии с положениями латентно–структурного анализа оценки испытуемых учитывают уровень трудности используемых при тестировании заданий и выдаются в виде тестовых баллов, рассчитанных с помощью математических моделей. В зависимости от числа оцениваемых параметров тестируемых различают несколько видов математических моделей современных тестов: однопараметрическую, двух–параметрическую, трехпараметрическую и др. Качество тестов, конструируемых на основе этих моделей, значительно улучшается, задания подбираются таким образом, чтобы обеспечить возможность проявления испытуемыми не только знаний, умений и навыков, но и других характеристик, проверка которых может быть заложена в спецификациях тестов.

В IRT вводится представление о существовании взаимосвязи между наблюдаемыми результатами тестирования и латентными качествами испытуемых, такими как уровень учебных достижений по предмету на момент тестирования. В отличие от классической теории тестов, где индивидуальный балл тестируемого рассматривается как постоянное наблюдаемое число X i, в IRT латентный параметр трактуется как некоторая переменная (латентная переменная), начальное значение которой получается непосредственно из эмпирических данных тестирования (например, первичный балл). При этом латентные параметры (уровень подготовленности испытуемого θ i и уровень трудности задания β j ) рассматриваются как результат взаимодействия двух множеств значений, порождающих наблюдаемые итоги выполнения теста. Элементами первого множества являются значения латентного параметра θ i– уровня знаний N испытуемый: (i = 1, 2, ..., N). Второе множество образуют значения латентного параметра β i, соответствующего разной трудности заданий теста (j = 1, 2, ..., n). На практике всегда ставится задача оценить по ответам испытуемых значения параметров θ и β. Для ее решения выбирается вид соотношения между этими параметрами (математическая модель).

Оказалось, что эмпирически наблюдаемые результаты X i и соответствующие им латентные значения уровня подготовленности испытуемых θ iсвязаны нелинейно. Переменный характер измеряемой величины трудности задания β j также указывает на возможность последовательного приближения ее к объективным оценкам параметров при помощи итеративных методов в процессе апробации. Выбором математической модели установливается взаимосвязь между эмпирическими результатами тестирования и значениями латентных переменных: θ – уровень знаний испытуемых и β – уровень трудности задания.

Однопараметрическая модель датского математика Г. Раша (G. Rasch) устанавливает зависимость между уровнем подготовленности испытуемого (θ i) и трудностью заданий (β j ) [248]. Он предложил ввести это соотношение в виде разности между параметром уровня знаний испытуемых и параметром трудности заданий теста: θ i−β j . При этом предполагается, что оба параметра оцениваются на одной и той же шкале логитов. Функция успеха, или вероятность правильного ответа Р j(θ) при тестировании задается простой логистической моделью:

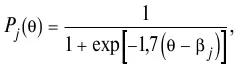
где параметром является разность (θ−β j), абсолютная величина которой представляет в логитах расстояние между уровнем знаний данного испытуемого и уровнем трудности данного задания. Если эта разность велика и отрицательна, то такое трудное задание бесполезно для измерения уровня знаний данного тестируемого, в то же время если эта разность велика и положительна, то задание тоже не представляет интереса, оно неэффективно, так как такой уровень трудности данным тестируемым уже хорошо освоен.

Из логистической функции видно, что P j(θ) растет с ростом параметра θ испытуемых, так как чем выше уровень знаний тестируемых, тем выше вероятность правильного ответа на–е задание теста. Взаимосвязь между этими параметрами хорошо просматривается по характеристической кривой–го задания теста, вид которой представлен на рис. 7. Точка перегиба соответствует равенству уровня знаний тестируемого и уровня трудности тестового задания, θ=β j, вероятность правильного ответа при этом равна 0,5. Вероятность правильного ответа для хорошо подготовленных испытуемых стремится к 1, а для плохо подготовленных – к 0. Увеличение трудности задания на некоторую константу с > 0 смещает характеристическую кривую вправо, с прежней вероятностью на такое задание теперь сможет ответить тестируемый с другим уровнем знаний, равным (θ + с).

В однопараметрической модели вероятность правильного ответа на задания выражается посредством логистической функции, после введения которой симметрично возникла математическая модель, описывающая вероятность правильного ответа в зависимости от трудности заданий [196]. Аналогично по формуле рассчитывается вероятность Р i(β) правильного ответа i – го испытуемого на разные по трудности задания теста: