Надежда Ефремова - Тестовый контроль в образовании

По такой упорядоченной матрице рассчитываются доли правильных р i и неправильных q i ответов испытуемых:

p i = X i /n, q i = 1 – P i , где ( i= 1, 2, ..., N).

Аналогично рассчитываются доли правильных и неправильных ответов на задания теста:

P j= R j/N и q j= 1 – P j , где ( j= 1, 2, ..., n).

Сначала рассчитывается первичный балл каждого тестируемого:

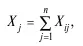
являющийся только начальной оценкой уровня подготовки учащихся или студентов, и определяется число правильных ответов на каждое задание теста:

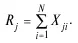
Это позволяет сделать первичную оценку трудности каждого задания. Следует иметь в виду, что показатель трудности задания R j удобен до тех пор, пока число испытуемых N в разных группах остается неизменным. Если в группах число испытуемых меняется, то необходимо пользоваться нормированным статистическим показателем трудности P j , он не зависит от N и характеризует долю правильных ответов:

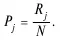
Оценка латентных параметров в большинстве случаев проводится в предположении нормальности распределения эмпирических данных как по множеству испытуемых, так и по множеству заданий.

Для лучшей наглядности информация о распределении первичных баллов тестируемых может быть представлена в виде гистограммы или кривой распределения. Максимальная частота выбора правильного результата (число тестируемых, набравших соответствующий балл) должна находиться в центре кривой, к краям частота снижается. Проверка нормальности распределения значений индивидуальньж баллов X i (мера центральной тенденции) желательна при создании нормативно–ориентированных тестов. Одной из наиболее простых мер проверки центральной тенденции является среднее арифметическое; если его значение соответствует 50% общей суммы баллов для данного теста, то условие нормализации выполнено.

После этого определяются значения дифференцирующей способности α j, как это было указано ранее. Найденные для всех заданий значения α jпозволяют перейти к оценке уровня знаний испытуемых, или уровня подготовленности, – латентного параметра θ. В качестве начального значения латентного параметра выбирается индивидуальный балл тестируемого X i.

Аналогично проводится определение начального значения латентного параметра трудности задания β j по значению R j. Затем вычисляются стандартные ошибки измерений θ и β, строятся характеристические и информационные кривые, рассчитывается показатель эффективности заданий и другие параметры. Расчет статистических показателей заданий теста, как правило, проводится по специальным автоматизированным программам и не требует специальной подготовки [197].

Схематически целевая и эмпирическая функции (для разного числа заданий) в процессе разработки и совершенствования теста за счет добавления заданий показаны на рис. 9. Правило определения длины теста указывает, что в процессе моделирования необходимо собирать статистику и подсчитывать дисперсию индивидуальных баллов тестируемых после каждого удлинения теста, наблюдая за изменением информационной функции теста.

Как только (при удовлетворительном заполнении области под целевой информационной функцией и при высокой содержательной валидности) дисперсия

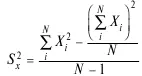
прекращает изменяться, можно найти оптимальную длину теста (X i– число правильных ответов i – го испытуемого; N – число испытуемых).

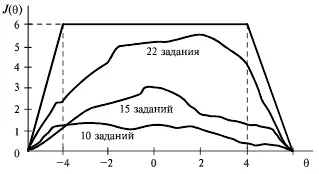
Рис. 9.Динамика информационной функции теста J(θ) – информационная функция; θ – уровень знаний

Апробация теста требует много времени, но обеспечивает высокий уровень качества теста. Верхняя часть кривой отражает стремление разработчиков создать тест, обеспечивающий равную точность оценок испытуемых в заданном интервале оценок на шкале логитов.

Для обработки статистических данных по результатам применения теста необходимо использовать ту же модель, что и при конструировании теста. Благодаря свойству инвариантности устойчивые оценки параметров тестовых заданий в IRT получаются на любой репрезентативной выборке (порядка 200 человек), даже если она существенно отличается от планируемой. На В –оси латентной переменной – информационная функция в пределах от–3 до +3 логитов соответствует диапазону оценки уровня знаний, определяемого нормативно–ориентированными тестами.

Следует обратить внимание на то, что при одной и той же спецификации заполнение области кривой под целевой информационной функцией может быть получено разными способами за счет использования разных по трудности тестовых заданий. В разрабатываемом тесте задания варьируются по трудности и дифференцирующей способности на основе одной и той же спецификации теста. Это особенно следует учитывать при создании параллельных тестов, когда крайне важно обеспечить равную трудность различных вариантов в соответствующих точках на оси переменной измерения, при переработках теста, исследованиях эффективности различных форм тестовых заданий, сопоставлении методов отбора заданий из банка и в других случаях. Поэтому необходимы сопоставление эффективности различных тестов и выбор оптимального набора заданий, обеспечивающих планируемые свойства теста.

Надежность теста снижается при подборе преимущественно легких или трудных заданий, кроме того, тест не отражает содержание учебной дисциплины. Наибольшей могла бы быть надежность теста, составленного из средних по трудности заданий, однако тогда снижаются содержательная валидность и дифференцирующая способность теста. В свою очередь, стремление поднять валидность может привести к снижению надежности. В теории конструирования тестов этот случай достаточно подробно описан Ф. Лордом (F.M. Lord) [242].

Подбор заданий сбалансированной сложности позволяет удовлетворить требованиям оптимальной надежности и валид–ности теста. Расчет надежности достаточно сложен, а поэтому для практических целей рекомендуется более простой метод. Проводится повторное тестирование испытуемых в одинаковых условиях по одним и тем же тестам, а потом выполняется проверка на коррелирование результатов. При значениях корреляции 0,9 и выше надежность отличная; от 0,85 до 0,89 – очень хорошая; от 0,8 до 0,84 – хорошая; далее – удовлетворительная; ниже 0,5 – неудовлетворительная. В практике применяется очень мало тестов, имеющих надежность 0,8 [2].