Надежда Ефремова - Тестовый контроль в образовании

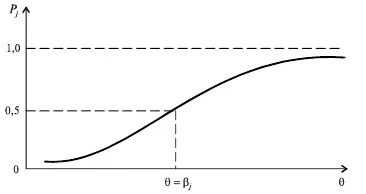
Рис. 7.Характеристическая кривая тестового задания

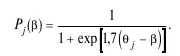
Вероятность правильного выполнения i -м испытуемым будет убывающей функцией в зависимости от трудности заданий. График функции Р i(β), или график индивидуальной кривой испытуемого, показан на рис. 8.

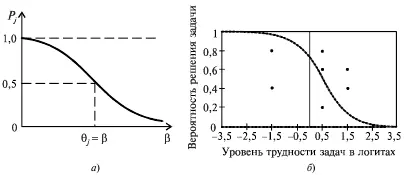
Рис. 8.Индивидуальная кривая испытуемого: а – теоретическая, уровень знаний 0,5; б – эмпирическая, уровень знаний 0,6

В точке перегиба кривой вероятность правильного ответа, как и на характеристической кривой задания, равна 0,5. В процессе обучения, по мере накопления знаний, индивидуальная кривая испытуемого смещается вправо.

Двухпараметрическая модель А. Бирнбаума (А. Birnbaum) [231] была получена путем добавления к параметрам трудности заданий теста их дифференцирующей способности ?. В последнее время обработку эмпирических данных рекомендуется проводить на основе двухпараметрической модели, чтобы кроме латентного параметра трудности заданий теста можно было бы в широком диапазоне дифференцировать уровни знаний разных учащихся. Дифференцирующая способность является одной из важных характеристик заданий теста и определяется разностью долей правильных ответов слабой и сильной частей испытуемых в группе достаточно большой выборки (около 100 человек). Методика расчета достаточно проста: берут 27% испытуемых, имеющих наибольшие баллы, и 27% имеющих низкие баллы, считают долю правильных ответов в каждой группе р ли р х . Затем определяют дифференцирующую способность для каждого задания данного теста: α j= p л− p x.

Например: на одно из заданий среди лучших правильно ответили 30 испытуемых из 40 (р л= 3/4), а среди худших правильный ответ у 10 из 40 (р х = 1/4), из чего следует, что α j= 1/2. Для других заданий расчеты делаются аналогично. Отметим, что для всех заданий теста значения дифференцирующей способности находятся в пределах от–1 до +1.

Вероятность правильного ответа на . – е задание в модели Бирнбаума записывается так:

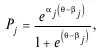
где θ – уровень знаний тестируемых (переменная); β j·– трудность j – го задания; – параметр, характеризующий дифференцирующую способность j – го задания; (θ – β j) – разность на шкале логитов между уровнем знаний учащегося и уровнем трудности j–го задания. При геометрической интерпретации его связывают с крутизной характеристической кривой в точке перегиба: чем круче кривая, тем больше дифференцирующая способность задания.

Совершенствование модели привело А. Бирнбаума к необходимости введения третьего параметра, учитывающего фактор угадывания правильного ответа. Новая модель стала называться логистической трехпараметрической. Ввиду большой сложности конструирования такого теста и статистической обработки результатов она не получила широкого распространения, так же как и метод наибольшего правдоподобия и метод моментов [250].

Для моделирования теста и, тем более, для создания системы адаптивного тестового контроля важную роль играет информационная функция теста, позволяющая задать на оси латентной переменной (логистической шкале) интервал, в котором проводится измерение уровня подготовки испытуемых. Бирнбаумом она представлена в виде

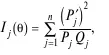
где I j (θ) – информационная функция; θ – уровень знаний испытуемого, латентная переменная; P j(θ) – вероятность правильного ответа на задание j; Q. (θ) = 1— P j(θ), Q – вероятность неправильного ответа на задание j; n – число заданий в тесте;

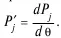
Информационная функция задает интервал, в котором работает данное задание, чем меньше этот интервал и круче характеристическая кривая, тем выше информативность и дифференцирующая способность такого задания. Это утверждение привносит дополнительные возможности в отбор заданий при формировании теста, позволяя варьировать диапазон заданий на шкале логитов. Введение информационной функции позволяет оценить точность педагогических измерений. Информативность задания обратно пропорциональна ошибке измерения, следовательно, речь может идти о дифференцированной оценке точности, обеспечиваемой j – м заданием теста данного уровня подготовленности θ i.Каждому уровню подготовленности в соответствие ставится количество получаемой при измерении информации. Отсюда следует, что наиболее информативно измерение подготовленности i-го испытуемого будет j – м тестовым заданием с уровнем трудности в точке перегиба при равенстве θ i=β j. Таким образом, чем ближе значение разности (θ i−β j) к нулю, тем эффективнее подобрано задание и меньше стандартная ошибка измерения уровня подготовленности испытуемого.

Для получения качественного теста необходима его апробация на предмет получения статистических характеристик, выявления трудности заданий, их дифференцирующей способности, характеристик теста в целом. Поэтому требуется проведение апроба–ционных тестирований, проверки трудности теста на выборках генеральной совокупности для выявления устойчивости показателей. После проведения апробационного тестирования выполняется математико–статистическая обработка результатов испытания, которая состоит из нескольких этапов.

Обработка данных начинается с выбора правил оценивания ответов испытуемых на задания теста. В большинстве случаев используется дихотомическая оценка. Оценку выполнения i -м испытуемым j – го задания обозначим X ij. Она может принимать значения 1 или 0, при этом i = 1, 2, ..., N,, где N – число учащихся или студентов; а j = 1, 2, ..., n, где n – количество заданий в тесте. Из значений X ijсоставляют матрицу эмпирических данных. Строки матрицы состоят из нулей и единиц, соответствующих ответам разных испытуемых, по столбцам располагаются профили ответов на каждое задание, т.е. столбцов должно быть столько, сколько заданий в тесте – n, а строк – сколько испытуемых – N. Матрицу данных тестирования (столбцы – число правильных ответов на каждое задание теста Rj, строки – правильные ответы тестируемых) упорядочивают, располагая Rj в порядке убывания результата. Строки матрицы меняют так, чтобы верхняя соответствовала обучаемому с минимальным индивидуальным тестовым баллом X i.