Сергей Капица - Парадоксы роста. Законы развития человечества

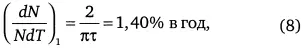
достигнутом в 1995 г., что согласуется с данными ООН, но дает несколько меньшее значение для абсолютной скорости роста при сравнении с табл. 1 (см. рис. 18).

Население нашей планеты в этот критический момент перехода Т 1равно:

N 1= К 2/2 = 5680 млн. (9)

На основе этих выражений легко определить предел N ∞, в два раза больший, чем N 1к которому в эпоху Сасимптотически стремится население Земли:

N ∞= 2N 1= πK 2= 11 360 млн. (10)

В рамках сделанных предположений это число представляет верхнюю оценку населения Земли в предвидимом будущем. Таким образом, глобальное взаимодействие приводит к ускорению и синхронизации процессов и на заключительной стадии демографического перехода — к сужению перехода и тем самым к снижению предела для населения Земли. Этот вывод находится в согласии с эмпирическими наблюдениями демографов. Рассмотрение N (Т) как аналитической функции указывает на асимптотическое поведение при T → ∞, когда N → N ∞, в предположении об отсутствии особенностей — полюсов или нулей — в обозримом будущем.

Начальный линейный рост дает оценку времени для эпохи антропогенеза — критической сингулярности в начале предыстории человечества, которая случилась:

T 0- T 1= π/2·Kτ = — τ√πN 1/2 = 4,2 млн лет назад, (11)

если использовать известное значение N 1и одно и то же значение τ = 45 лет для сингулярности в далеком прошлом и в настоящем. Несмотря на сделанные упрощения, данная оценка вполне согласуется с оценками времени Т 0в антропологии.

Интересно определить полное число людей, живших на Земле. Если переставить переменные в (6) и проинтегрировать:

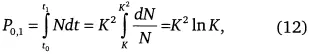
то получим число людей, живших от Т 0до нашего времени Т 1В оценках других авторов длительность поколения принята равной 20 годам, что ведет к оценке Р 0,1= 106 млрд [10]. Поэтому необходимо введение в (12) множителя 45/20 = 2,25:

Р 0,1= 2,25 К 2ln К = 90 млрд. (13)

Таким образом, в течение каждого из ln К = 11,0 выделенных периодов жило по 2,25 K 2= 8 млрд людей. Это число является инвариантным для числа людей, живших в экспоненциально сокращающихся циклах, а ln K указывает на число циклов.

Циклы можно получить, обобщая решение (6) в область комплексных переменных или же просуммировав экспоненциально сокращающиеся циклы:

ΔT = К τ ехр (-θ), (14)

где θ = |ln t| — номер цикла, определить длительность развития при К >> 1:

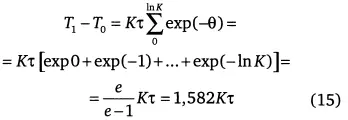
и сравнить ее с (11), где длительность равна Т 1- Т 0= π/2·Kτ = 1,571. В первом случае рост суммируется по гиперболической траектории, во втором — по (4) — N = K tan t/K.

Демографические циклы определяют периодичность развития всего человечества за 4–5 млн лет, включая проходящий по гиперболическому закону рост от конца антропогенеза до наших дней.

Для дальнейшего обзора результатов перейдем к переменной n = N/K:

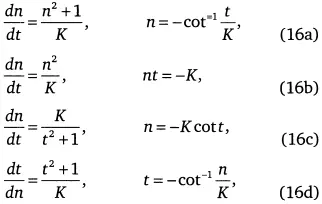
когда мерой численности становится К. Тогда уравнения для роста приобретают симметричный вид и видно сопряжение переменных n и t. Смена зависимой переменной в (16а) и (16d) видна при прохождении перехода, когда n становится независимой переменной вместо времени t, что выражено в уравнении роста (3).

Рост населения можно иллюстрировать геометрическим построением функции тангенса:

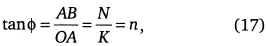
где угол Δφ = τ отображает течение времени, а приращение населения ΔN = 1 (рис. 16).

Линейный рост будет продолжаться до φ A,B= Кτ = 1 и N B= tan 1 в точке В на касательной АС. Дальнейший рост N = К(π/2 — φ) -1будет проходить по гиперболе, при которой время асимптотически стремится к π/2, а население достигнет значения N c= К 2. Когда система приближается к моменту особенности, то от уравнения (16а) следует переходить к уравнению (16d), чтобы описать рост при прохождении особенности в течение эпохи С. Построение показывает, что после перехода от линейного к гиперболическому росту на эпоху Востается в два раза меньше времени, чем на начальную эпоху А. Вывод этого соотношения для всей эпохи В(см. рис. 19) построен при К = 7, когда время от Т 0до Т 1разделено на 11 интервалов, и поскольку к/2 = 1/7, то N c= К 2=49. Однако даже при таком малом значения К, когда In K = In 1,95 дает хорошую оценку для числа демографических циклов, 1 + In К ≈ 3. Таким образом нулевой цикл антропогенеза продолжался 7 единиц времени, первый цикл длился 3 и последний — одну единицу времени. Это построение показывает, как дискретность времени и населения приводит к появлению периодичности роста, выраженной в демографических циклах как главных эпохах развития человечества.

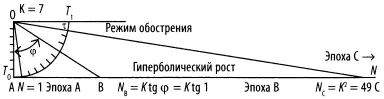
Рис. 19. Построение функции тангенса, показывающее пределы асимптотик роста

Линейный рост описывает поведение системы вблизи начальной сингулярности роста, начинающейся с N 0= 1 и положительных значений N. Далее следует рост по гиперболе и в конце — сингулярность демографического взрыва. Построение, когда переменные n и t при прохождении перехода меняются местами, мы оставляем читателю.

На рис. 18 показаны функции, описывающие рост системы при К = 1, которые появляются при построении решения, начинающегося с сингулярности в эпоху А, переходящего затем в эпоху Вгиперболического роста и завершающегося эпохой С. Асимптотический переход решений, описывающий рост в начале развития и на его конечном участке, получим, обратившись к рядам для функции cot (t/K) и cot -1(t/K):

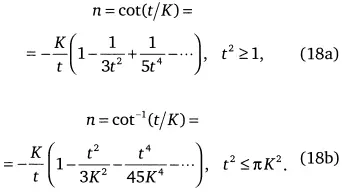
Эти функции пересекаются в точке А, посередине роста при логарифмическом представлении между временем T 0и T 1соответствующей наступлению неолита:

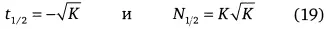
под углом 2/(3K) практически гладко при больших значениях К.

Очевидно, что решение можно строить, отсчитывая время от T 0— от эпохи антропогенеза Апри t 0= 0. Тогда, исключив t из (15с), получим одно автономное дифференциальное уравнение, описывающее рост в зависимости от состояния системы, которое определяется населением Земли и где последний член добавлен с тем, чтобы рост в эпоху А никогда не был меньше одного гоминида при Δt = τ.