Сергей Капица - Парадоксы роста. Законы развития человечества

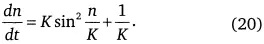
Интегрируя (20) при значениях K > 1 и начальных условиях t 0= n 0= 0, получим решение:

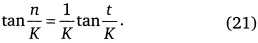
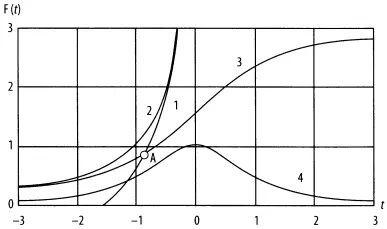
Рис. 20. Функции F (t), описывающие рост

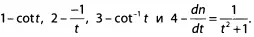
Это решение показывает симметрию переменных N и T — населения и времени. Для развития в течение эпохи Ввдали от особенностей роста это выражено в (16в) и следует из сложности причинных связей в рамках развитых представлений о нелинейной динамике глобальной системы населения нашей планеты.

Для того чтобы выяснить устойчивость развития, следует обратиться к уравнению роста человечества (20). На основании (15) в линейном приближении устойчивость роста к возмущениям

δN = δN 0exp(λt) (22)

определит показатель Ляпунова λ развития неустойчивости в системе населения:

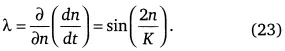
По этому критерию при λ > О движение неустойчиво до перехода. Только после него развитие системы становится асимптотически устойчивым и впредь таким и остается. Отметим, что в этих решениях значение констант роста К и τ не эволюционируют. Более полное определение устойчивости потребует введения распределений для n и обращения к методам статистической физики при обобщении развитой выше модели.

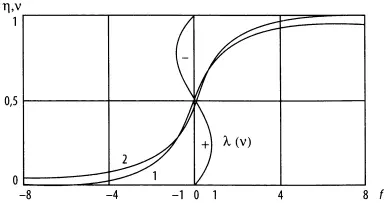
Рис. 21. Переходные процессы и устойчивость роста в линейном приближении

1 — логистический переход ν = 1/1+е -r; 2 — демографический переход η = 1/π соt -1T и λ (ν).

При гиперболическом росте мгновенное значение экспоненциального роста равно древности,

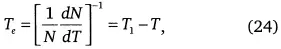
что и определяет скорость процессов развития в момент времени Т.

В гиперболической хронологии мгновенный экспоненциальный масштаб времени роста линейной неустойчивости по Ляпунову зависит от древности и до демографического перехода равен удвоенному времени роста неустойчивости:

T e= 2τ/λ (25)

Однако наличие выделенных антропологами и историками демографических циклов указывает на глобальную устойчивость с малыми отклонениями системы от предельной траектории роста.

Наконец, из (15) следует, что после каждого цикла до демографического перехода остается приблизительно половина времени длительности цикла:

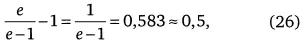
что вполне подтверждается данными истории и антропологии (см. табл. 2, с. 74).

Асимптотические решения для нелинейных задач приобретают, как заметил Я. Б. Зельдович, то же значение, что частные решения для линейных задач, где действует принцип суперпозиции. В нашей задаче автомодельные решения имеют асимптотический характер, при котором значение некоторых параметров оказываются несущественным, подобно тому как в частных решениях линейных задач происходит вырождение по некоторым параметрам. Так, частота колебаний в линейной задаче не зависит от их амплитуды.

В некоторых случаях независимость от параметра позволяет от уравнений в частных производных перейти к обыкновенным дифференциальным уравнениям. Именно это происходит в задаче о росте человечества, когда в нелинейном уравнении (6) можно пренебречь пространственным распределением населения, поскольку в первом приближении перемещение на конечной по размерам Земле — миграция населения — не влияет на само число людей.

В заключение заметим, что изложенная теория рассматривает задачу о росте и развитии демографической системы в асимптотическом приближении. Из этого следует, что в этом приближении ресурсы не влияют на глобальное взрывное развитие. Поэтому ограничение роста и переход к стабилизации населения мира обязаны внутренним процессам, выраженным в принципе демографического императива, и не подчиняется внешним, в первую очередь ресурсным факторам.

Здесь, несомненно, открывается обширное поле для исследования этой проблемы во всеоружии современных методов статистической физики, теории фазовых переходов и неравновесных систем. Более того, эта задача во многом подобна задачам космологии. Но она гораздо ближе к нам, поскольку имеет огромное значение для фундаментального понимания истории и экономики. Выразим поэтому уверенность, что эта проблематика приведет к развитию своих методов и в теоретической физике.

1. Капица СП., Курдюмов СП., Малинецкий Г. Г. Синергетика и прогнозы будущего. — М.: Наука, 1997.

2. Капица СП. Общая теория роста человечества. — М.: Наука, 1999.

3. Kapitza S. P. Global Population Blow up and After. The demographic revolution and information society. A Report to the Club of Rome. — Hamburg: Global Marshall Plan Initiative; Moscow: Tolleranza, 2007.

4. Медоуз Д. и др. Пределы роста. — М.: ИКЦ, 1990.

5. Ясперс К. Смысл и назначение истории. — 2-е изд. — М.: Республика, 1994.

6. Braudel F. On History. — Chicago: University of Chicago Press, 1980.

7. Бродель Ф. Материальная цивилизация, экономика и капитализм XV–XVIII вв. 1–3 т. — М.: Весь Мир, 2007.

8. Конрад Н. Е. Запад и Восток. — 2-е изд. — М.: Наука, 1972.

9. Дьяконов И. М. Пути истории. От древнейшего человека до наших дней. — М.: Восточная литература, 1995.

10. Гиббон Э. История упадка и разрушения Римской империи. — СПб.: Наука, 2000.

11. Мясников B.C. Российский анти-Мальтус // Вестник Российской академии наук, 2000. № 7.

12. Fucuyama F. The End of History and the Last Man. — New York, 1992.

13. Шкловский И. С. Вселенная, жизнь, разум. 6-е изд. — М.: Наука, 1987.

14. Баренблатт Г. И., Подобие, автомодельность, промежуточная асимптотика. — М.: Наука, 1985.

15. Баренблатт Г. И. Автомодельные явления — анализ размерностей и скейлинг. — Долгопрудный: Интеллект, 2009.

16. Самарский А. А., Галактионов В. А., Курдюмов С. П., Михайлов А. П. Режимы с обострением в задачах для квазилинейных параболических уравнений. — М.: Наука, 1987.

17. Режимы с обострением. Эволюция идеи/ Под ред. Г. Г. Малинецкого. — М.: Наука, 1999.

18. Хакен Г. Синергетика. Иерархия неустойчиво-стей в самоорганизующихся системах и устройствах. — М.: Мир, 1985.

19. Поллард К. Что нас делает людьми? // В мире науки, 2009. № 7.

20. Манелис Г. Б. Частное сообщение.

21. Chesnais J-С. The Demographic Transition. Stages, Patterns and Economic Implications. — Oxford: Oxford university press, 1992.