Норберт Винер - Кибернетика или управление и связь в животном и машине

Оправдание этой процедуры следующее. Распределение массы, равное

1 в точках 2π n ,

—1 в точках (2 n +1)π и

0 во всех остальных точках,

если его подвергнуть гармоническому анализу, будет [c.277]содержать косинусоидальную составляющую с частотой 1 и не будет иметь синусоидальной составляющей. Точно так же распределение массы, равное

1 при (2 n +1/2)π,

—1 при (2 n —1/2)π и

0 во всех остальных точках,

будет содержать синусоидальную составляющую с частотой 1 и не будет иметь косинусоидальной составляющей. Оба распределения будут содержать также составляющие с частотами N ; но поскольку исходная наша кривая не содержит или почти не содержит таких частот, эти члены будут незаметны. Это значительно упрощает наше гетеродинирование, так как нам нужно умножать лишь на множители +1 или —1.

Мы нашли метод гетеродинирования очень полезным при гармоническом анализе мозговых волн, когда в распоряжении имеются лишь ручные средства и когда объем работы становится подавляющим, если выполнять все шаги гармонического анализа без помощи гетеродинирования. Все наши первые исследования по гармоническому анализу спектров мозга выполнены методом гетеродинирования. Но поскольку со временем появилась возможность применять цифровую вычислительную машину, для которой объем работы не столь существен, многие из последующих анализов были проведены прямыми методами, без гетеродинирования. Однако еще немало работы придется делать в местах, где нет цифровых вычислительных машин, и я не считаю метод гетеродинирования устаревшим в практическом отношении.

Я привожу здесь куски одной автокорреляционной кривой, полученной при наших исследованиях. Ввиду того, что она охватывает большую серию данных, воспроизвести ее полностью затруднительно, и мы даем только се начало, в окрестности τ =0 и один из дальнейших кусков.

Рис. 11 изображает результат гармонического анализа автокорреляционной кривой, часть которой показана на рис. 9. В данном случае результат был получен на быстродействующей цифровой вычислительной машине [192], [c.278]но мы обнаружили хорошее согласие между этим спектром и вычисленным ранее вручную методами гетеродинирования, по крайней мере вблизи сильной части спектра.

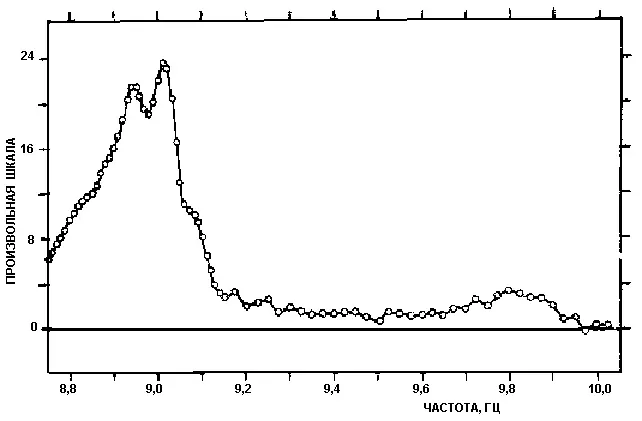
Рис. 11. Спектр

Рассматривая кривую, мы обнаруживаем замечательное падение мощности в окрестности частоты 9,05 гц . Точка, в которой спектр по существу исчезает, выражена весьма отчетливо и дает объективную величину, которая может быть проверена с гораздо большей точностью, чем любая величина, встречавшаяся до сих пор в электроэнцефалографии. Существуют указания, что на других кривых, которые мы получили, но которые несколько сомнительны в своих подробностях, за этим внезапным падением мощности довольно скоро следует крутой подъем. Таким образом, кривая имеет здесь как бы впадину. Но даже если догадка не верна, многое говорит за то, что концентрация мощности в пике соответствует отсасыванию мощности из области, где кривая идет низко. Стоит отметить, что в полученном спектре основная часть пика лежит в диапазоне шириной 1/3 гц . Любопытно, что на другой электроэнцефалограмме того же субъекта, записанной через четыре дня, ширина пика почти не изменилась и, насколько можно судить, форма его также сохранилась в [c.279]какой-то мере. Есть основание полагать, что у других субъектов ширина пика будет другой и даже меньшей. Для вполне удовлетворительной проверки этого необходимы дальнейшие изыскания.

Весьма желательно, чтобы исследования, здесь упомянутые, были продолжены более точными инструментальными работами, с лучшими приборами, и чтобы благодаря этому гипотезы, высказанные здесь, могли быть окончательно подтверждены или окончательно опровергнуты.

Теперь я хочу перейти к вопросу выборки. Для этого мне понадобятся некоторые идеи из моих предыдущих работ об интегрировании в пространстве функций [193]. С помощью этого аппарата мы сможет построить статистическую модель непрерывного процесса с заданным спектром. Хотя такая модель не воспроизводит в точности процесса формирования мозговых волн, она достаточно близка к нему, чтобы доставить статистически значимую информацию о том, какой среднеквадратической ошибки можно ожидать в спектрах волн, подобных представленному выше.

Здесь я сформулирую без доказательств ряд свойств некоторой действительной функции х ( t , α), уже излагавшихся в моей статье по обобщенному гармоническому анализу и в других работах [194]. Действительная функция х ( t , α) зависит от переменной t , изменяющейся от —∞ до ∞, и от переменной α, изменяющейся от 0 до 1. Она изображает одну пространственную координату броунова движения, зависящую от времени t и параметра α статистического распределения. Выражение

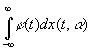(10.09)

определяется для всех функций φ( t ) класса Лебега L 2, [c.280]в интервале от —∞ до +∞. Если φ( t ) имеет производную, принадлежащую L 2, то выражение (10.09) понимается как

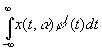(10.10)

и затем определяется для всех функций φ( t ) из L 2некоторым вполне определенным предельным процессом. Другие интегралы

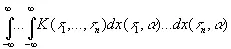(10.11)

вводятся аналогичным образом.

Основная теорема, используемая нами, утверждает, что

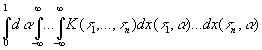(10.12)

можно найти, положив

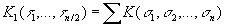, (10.13)

где переменные τ k образуются всеми возможными способами путем отождествления всех пар переменных σ k , друг с другом (если n четно) [195], и образовав

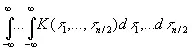(10.14)

Если n нечетно, то

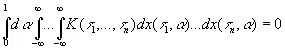(10.15)

Другая важная теорема, касающаяся этих стохастических интегралов, гласит: пусть F { g } — функционал [c.281]от g ( t ), такой, что F [ x ( t , α)] есть функция, принадлежащая к L по α и зависящая только от разностей x ( t 2, α)— х ( t 1, α); тогда для любого t 1и почти всех α