Александр Петров - Гравитация От хрустальных сфер до кротовых нор
- Название:Гравитация От хрустальных сфер до кротовых нор
- Автор:
- Жанр:
- Издательство:«Век 2»
- Год:2013
- Город:Фрязино
- ISBN:978–5–85099–190–6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Петров - Гравитация От хрустальных сфер до кротовых нор краткое содержание
Гравитация От хрустальных сфер до кротовых нор - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Чтобы опровергнуть и эти возражения недавно (результаты опубликованы в 2011 году) в центре синхротронного излучения Курчатовского института был произведён опыт. Исследовали излучение сгустка электронов, разогнанного почти до скорости света и запущенного по искривлённой траектории. В этом случае есть большое ускорение, а именно тогда происходит эффективное излучение. По баллистической гипотезе скорость света должна быть близка к двойной световой — 2 с . Эффект огромный, его нельзя не заметить. Провели два типа экспериментов. Для первого — свет разделили на два пучка: один пустили напрямую, а второй — через стеклянную пластину, чтобы установить, изменяет ли переизлучение скорость света Затем оба пучка сравнили. Разницы в скорости не было найдено! Во втором эксперименте скорость синхротронного излучения измерили напрямую. Как и ожидалось, она с высокой точностью оказалась равной своему обычному значению — с , никак не 2 с . Можно сказать, что это ещё одна непосредственная проверка второго принципа.
Пространство Минковского
Тогда нарушается закон причинно-следственной связи, закон, от которого я совершенно не собирался отказываться из‑за каких‑то паршивых попугаев, да ещё дохлых вдобавок…
Аркадий Стругацкий, Борис Стругацкий «Понедельник начинается в субботу»
Как мы уже отметили, в СТО пространство и время нужно рассматривать как единый четырёхмерный континуум — его называют пространством Минковского. Тогда непривычные (для бытового восприятия) свойства теории объяснять и интерпретировать значительно легче. Пространство Минковского представляют в виде диаграммы
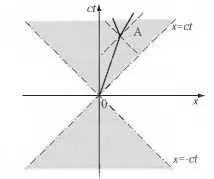
Рис. 5.2. Путь частицы на диаграмме пространство–время
с временной и пространственными осями. На временной оси в качестве отсчёта используется время, умноженное на скорость света — ct, это упрощает анализ, поскольку все данные имеют одинаковую размерность. Пространственные координаты, также для простоты, часто представлены только координатой x, хотя, конечно, подразумеваются все три. Кроме того, в отличие от общепринятых диаграмм, здесь роль функции играет время, а аргумента — пространственные координаты.
Диаграмма пространства Минковского, точно так же, как обычные диаграммы, используется для отображения в виде графика пути, который проходит материальная частица с течением времени. Если частица движется равномерно и прямолинейно — её путь будет прямой линией, а котангенс угла наклона к оси x равен скорости частицы в долях скорости света. На рис. 5.2 изображён путь такой частицы от начала координат до точки А. Прямые, направленные под углом 45°, отображают пути фотонов, движущихся со скоростью света как через начало координат, так и через точку А в разные стороны. Позже мы определим такие «фигуры» как световые конусы. Движение частицы от точки А возможно только внутри конуса, поскольку её скорость не может превышать световую.
Если частица движется произвольно, то её путь будет представлен кривой, а котангенс угла наклона касательной к оси x в какой‑либо точке будет равен скорости частицы в момент, соответствующий этой точке.
Как в СТО, так и в общей теории относительности (мы увидим это позднее) ключевым понятием является метрическое пространство. Под этим понимается некое множество точек, переход между которыми осуществляется непрерывным образом и определено понятие расстояния между ними. Вспомним обычное пространство Евклида. Квадрат расстояния r между началом координат и точкой с декартовыми координатами х, у, z определяется по правилу: r 2 = х 2 + у 2 + z 2 . Эта величина всегда положительная, за исключением случая, когда длина равна нулю.
Пространство Минковского тоже метрическое. Однако в нем расстояние между двумя точками называется интервалом и определяется непривычным образом. Квадрат интервала s между началом координат и какой‑либо точкой 4–мерного пространства–времени (рис. 5.2) определяется по правилу:
s 2= c 2 t 2 - х 2 - у 2 - z 2 = c 2 t 2 - r 2 .
Временную координату ct и пространственные координаты Декарта х, у, и z , представляющие единую координатную сетку в пространстве Минковского, обычно называют координатами Лоренца. Как видно, временная и пространственные части в определении интервала входят с разными знаками. Из‑за этого квадрат интервала может быть положительным, нулевым и даже отрицательным. Пространства, в которых расстояния определяются таким образом, называются псевдоевклидовыми.
Итак, пространство Минковского — это псевдоевклидово метрическое пространство, объединяющее время (длительность) и пространство (протяжённость, 3–мерное пространство Евклида).
Точки в пространстве Минковского называют событиями или мировыми точками. Таким образом, каждой мировой точке соответствует момент времени и точка в 3–мерном пространстве. А интервал — это расстояние между двумя мировыми точками или, в ряде интересных случаев, промежуток времени между двумя событиями.
Теперь попытаемся понять, как в рамках исходной системы отсчёта в пространстве Минковского выглядит другая инерциальная система отсчёта. Оси 0 ct и 0 x (см. рис. 5.2) в исходной системе образуют базис. Путь наблюдателя, связанного с исходной системой, направлен вдоль оси 0 ct. Для него же ось 0 x и параллельные ей линии — это сечения одновременности. Наблюдатель другой инерциальной системы движется прямолинейно и равномерно по отношению к первой. Тогда ясно, что его путь направлен вдоль наклонной прямой, например, 0 A на рис. 5.2. Для движущегося наблюдателя сечения одновременности также наклонятся. Остаётся сделать вывод: чтобы перейти к базису движущейся инерциальной системы отсчёта нужно осуществить поворот исходного базиса. При этом угол поворота соответствует относительной скорости между системами. Вспомним, что две системы отсчёта связаны преобразованиями Лоренца. Именно поэтому такие повороты базиса называют лоренцевыми вращениями.
На рис. 5.3 на диаграмме пространства Минковского изображён базис неподвижной системы K с не штрихованными координатами, и базис движущейся в направлении оси 0 x со скоростью V инерциальной системы отсчёта K’ с штрихованными координатами. Теперь выпишем преобразования Лоренца от одних координат к другим:
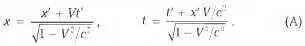
Интервал:
Закладка:







