Александр Петров - Гравитация От хрустальных сфер до кротовых нор

Преобразования дают возможность заключить, что обе системы отсчёта эквивалентны. Действительно, если выразить штрихованные координаты через не штрихованные, то получим те же самые преобразования:

с заменой знака «плюс» перед V на «минус» — по отношению к штрихованной системе не штрихов энная движется в противоположном направлении.

Одно из достоинств геометрической интерпретации пространства Минковского состоит в том, что лоренц-инвариантность выражается в инвариантности относительно лоренцевых вращений. В частности, значение интервала, записанного выше, не изменяется после поворота базиса, хотя теперь выражается через новые (штрихованные) координаты нового базиса. Чтобы убедиться в этом нужно лоренцевы преобразования (А) подставить в выражение для квадрата интервала, записанного выше. В результате получим:

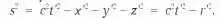
то есть s = s'.

В инвариантности интервала нет ничего удивительного — это лишь геометрическое свойство пространства Минковского, а не следствие каких‑то принципов. Действительно, поскольку интервал — это длина в метрическом пространстве, то эта величина не зависит от способов измерения (использования той или иной координатной сетки). Замечательно другое — известные геометрические свойства псевдоевклидовых пространств оказались весьма полезными для описания СТО.

Эффекты сокращения длины, замедления времени, сложение скоростей в СТО являются следствием лоренц-инвариантности. Остановимся на первых двух. Рассмотрим линейку, собственная длина которой l 0 — это длина в её системе покоя. Пусть система покоя для выбранной линейка — это система K' , которая движется относительно нас (системы К) со скоростью V . Тогда, если кон

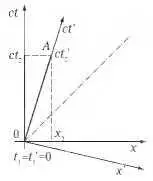
Рис. 5.3. Переход к другой инерциальной системе на диаграмме пространства Минковского

цы линейки имеют координаты x 1 ' и x 2 ', то l 0 = x 2 ' - x 1 '. Определим длину этого отрезка с точки зрения наблюдателя системы K. Для этого нужно в один и тот же (!) момент времени t определить координаты концов линейки x 2 и x 1 в системе К. Тогда для нас длина линейки буде иметь величину l = x 2 - x 1 . Чтобы определить каждое из значений x 2 и x 1 через соответствующие штрихованные координаты используем первую часть преобразований Лоренца (Б) каждый раз с одним и тем же значением t . Затем составим разницу и получим l = l 0 sqrt(1-V 2 /c 2 ) , то есть для нас (покоящейся системы K) движущаяся линейка становится короче.

Подтвердим вывод о замедлении времени. Находясь в системе К будем отслеживать ход часов в системе К' которые находятся в точке х'. Для нас часы в системе К идут одинаково во всех точках, поэтому часы системы K' можно сравнивать с любыми нашими. Не теряя общности, можно предположить, что х' = 0 и моменты первого сравнения в обеих системах также нулевые: t 1 ' = t 1 = 0 .

Вопрос в том, как начнут разниться показания в любой следующий момент сравнения t 2 (а для системы K' — t 2 '). Теперь удобнее использовать вторую часть преобразований Лоренца (А). Получаем t 2 = t 2 '/sqrt(1-V 2 /c 2 ) . Как видно, показания часов в нашей системе К будут больше, чем в К', хотя в обоих случаях отсчёт начинался с нуля. Таким образом, движущиеся часы идут медленнее.

На этом этапе важно сделать замечание. Мы все больше убеждаемся, что пространство и время физически объединены в единое целое — пространственно–временной континуум. Действительно, и пространственные, и временные координаты участвуют в единых преобразованиях; инвариантная величина интервал построена как из временных промежутков, так и из пространственных отрезков. Несмотря на это, и пространство, и время сохраняют свою физическую сущность — протяжённость и длительность. Формально это различие состоит в том, что временная часть входит в интервал со знаком «плюс», а пространственная — со знаком «минус».

Мы уже отметили, что квадраты интервалов могут быть положительными, нулевыми и даже отрицательными. Для положительных — временная часть превосходит пространственную, и они называются времениподобными. Нулевые соответствуют распространению света и называются светоподобными ; совокупность светоподобных, представляющая распространение световых лучей из какой‑либо мировой точки, образует, так называемый, световой конус в пространстве Минковского. На рис. 5.4 такой световой конус относится к началу координат и делит прост ранет в о–время на две части: внутри и вне конуса. Наконец, для отрицательных квадратов интервалов, пространственная часть превышает временную, и они называются пространственноподобными.

Для нас более интересны времениподобные интервалы. Почему? Отрезок прямой 0 А , соединяющий мировую точку внутри конуса и начало координат на рис 5.4 вполне можно интерпретировать как путь материальной частицы, движущейся прямолинейно и равномерно. Скорость её меньше скорости света, и поэтому путь находится внутри конуса. Квадрат интервала между точкой А и началом координат s 2 = c 2 t 2 - х А 2 — положительный, и это относится ко всем мировым точкам внутри конуса, скажем А'. Наклон соответствующих отрезков пути меньше, чем у светового конуса. Если бы мы попытались интерпретировать отрезки пути с наклоном больше, чем у светового конуса, как путь материальной частицы, то

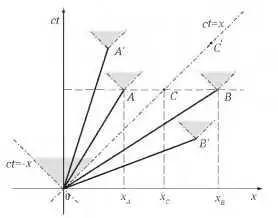
Рис. 5.4. Интервалы в пространстве Минковского

нужно было бы говорить о скоростях больших скорости света. Но для материальной частицы это невозможно, мы об этом ещё скажем.

Продолжим обсуждение времениподобных интервалов. На рис. 5,4 отрезок на временной оси, скажем, от начала координат до точки ct, определяет, конечно, такой интервал. В чем его смысл? Он соответствует наблюдателю, который покоится в этой инерциальной системе отсчёта, а соответствующий интервал определяет промежуток времени жизни наблюдателя между этими событиями: s = ct. После лоренцева вращения этот отрезок станет наклонным. (Другими словами: в другой инерциальной системе этот наблюдатель будет двигаться прямолинейно и равномерно.) Однако, в силу лоренц–инвариантности значение интервала для этого отрезка не изменится, хотя примет другое выражение: s = (c 2 t' 2 - х' 2 ) 1/2 . Это позволяет сделать важный вывод, давайте его зафиксируем: