Александр Петров - Гравитация От хрустальных сфер до кротовых нор

В хронометрической теории есть также решения, описывающие объекты типа чёрных дыр. Однако вспомним, что в этой теории нет предельной скорости, возможно распространение взаимодействий со скоростью большей, чем скорость света и даже мгновенно. Если бы эта возможность была в ОТО, то само понятие горизонта событий потеряло бы смысл, поскольку появляется возможность покинуть объект, находясь и на горизонте событий, и под ним. При этом появляются противоречия, связанные с термодинамикой системы, такие как уменьшение энтропии. Сейчас не известны все решения для чёрных дыр в теории Хоржавы в силу её молодости, однако среди известных есть такие, которые позволяют избежать этих осложнений. Оказывается, что в чёрной дыре в рамках хронометрической теории может быть так называемый универсальный горизонт. Он находится под горизонтом событий («ближе» к сингулярности) и замечателен тем, что поверхности постоянного времени, находящиеся под ним, не пересекают его. Это означает, что сигнал даже бесконечной скорости (мгновенный) не может выйти из- под этого промежуточного горизонта. А для таких объектов вышеупомянутые противоречия снимаются.

На рис. 12.2 представлена так называемая диаграмма Пенроуза чёрной дыры Шварцшильда. Точки i - и i + представляют всю временную бесконечность прошлого и всю временную бесконечность будущего, точка i 0 объединяет всю пространственную бесконечность. Прямая В i + является горизонтом событий шварцшильдовой чёрной дыры — это

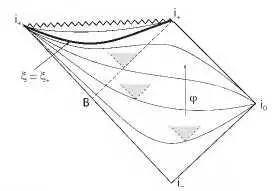
Рис. 12.2. Диаграмма хронометрической чёрной дыры

видно из расположения световых конусов. Действительно, квадрат В i + i 0 i - — это все внешнее пространство–время вне горизонта событий, в то время как треугольник i + Bi + — это пространство–время под горизонтом событий, откуда сигнал не может выйти во внешнюю область, и где ломаная линия — это сингулярность r = 0. На диаграмму шварцшильдовой дыры наложена диаграмма чёрной дыры хронометрической теории. Все кривые, соединяющие i 0 и i + , — это сечения постоянного поля хронона φ = const, то же самое, постоянного времени (одновременности). Жирная дуга — это тот самый универсальный горизонт ξ=ξ *, под ним, ближе к сингулярности, дуги i + i + , соединяющие концы ломаной линии — это тоже сечения постоянного времени (одновременности). Ясно, что если сигнал в хронометрической теории распространяется даже мгновенно, то есть вдоль сечений одновременности, то он не сможет пересечь универсальный горизонт и покинуть хронометрическую чёрную дыру.

Космология. В масштабах Вселенной теория Хоржавы также имеет шанс заявить о своей жизнеспособности. Обсудим космологические решения в новой теории. Они будут примерно такими же, как в ОТО, с той разницей, что вместо обычной гравитационной постоянной G будет фигурировать эффективная гравитационная постоянная G E . Теперь вспомним модифицированный закон Ньютона, о котором говорилось выше. Там появляется своя эффективная гравитационная постоянная, отличная от G, обозначим её G I . Сделаны оценки для разницы: |G I‑GE | ≤ 0,1. Нет запрета на то, что в будущем будет определена значимая величина для этой разницы, но так же возможно, что она будет исключена.

На основе ОТО разработана хорошо согласованная с наблюдениями теория космологических возмущений. Она позволяет, например, объяснить структуру, то есть распределение галактик и их скоплений в доступной наблюдениям области Вселенной. Тем не менее, если при повышении точности наблюдений будет обнаружена, скажем, анизотропия, не предсказанная ОТО, то это повод обратиться к теории Хоржавы. Теория Хоржавы настолько молода, что вряд ли её саму и выводы, сделанные на её основе, можно считать устоявшимися и всеми признанными. Несмотря на это, как теория в целом, так и выводы, представляются очень интригующими и важными.

На протяжении всего последнего столетия различные теории гравитации конструировались, так или иначе, как самостоятельные теории, т. е. «снизу». В последние десятилетия ситуация изменилась: построение теорий гравитации стимулируется развитием фундаментальных теорий, различные модели гравитации являются их частью и «выкристаллизовываются» в границах этих теорий. То есть их создание идёт «сверху». Будучи претендентами на «теории всего», фундаментальные теории включают и гравитацию.

«Теория всего» должна работать при самых фантастических условиях, в том числе при планковских энергиях.

Тогда все взаимодействия выступают как единое. Поэтому построение таких теорий в определённой степени — экстраполяция. А переход от теории, работающей при самых общих условиях, к условиям нашего мира будет её приближением, которое называется низкоэнергитическим. Как минимум, наблюдательные эффекты в «приближённой теории всего» должны иметь место в наблюдаемом нами мире. «Гравитационная часть теории всего» в низкоэнергетическом пределе приобретает привычный для нас вид, и она должна выдержать все тесты, которые выдержала ОТО. Заметим, что некоторые варианты «теории всего» в низкоэнергетическом пределе в качестве гравитационной части содержат ОТО в точности.

Важное свойство фундаментальных теорий заключается в том, что, как правило, как на космологических масштабах, так и на масштабах микромира используется размерность пространства–времени больше, чем 4. Концепция многомерного пространства необходима, например, для теории суперструн, которая, по общему признанию, представляет собой наиболее перспективную теорию высоких энергий, объединяющую квантовую гравитацию и теорию так называемых калибровочных полей. Низкоэнергетические следствия этой теории требуют, например, (9+1) — мерного фундаментального пространства–времени (иногда (10+1) — мерного), в то время как другие размерности запрещены.

Но как же тогда быть, мы же ощущаем только 3 пространственных и одно временное измерение? На микромасштабах дополнительные измерения компактифицированы (как бы свёрнуты в «трубочки»), и это причина, по которой они и не должны восприниматься нами. Такое пространство обладает симметриями по дополнительным измерениям, которым отвечают законы сохранения для различных зарядов, точно так же, как симметриям пространства Минковского отвечают законы сохранения для энергетических характеристик.