Стивен Вайнберг - Объясняя мир. Истоки современной науки

Другая причина того, что эти сочетания нот благозвучны, заключается в обертонах. Чтобы N 1-й обертон струны 1 имел ровно ту же частоту, что и N 2-й обертон струны 2, должно выполняться равенство vN 1/2 L 1= vN 2/2 L 2, и таким образом:

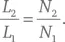
И вновь отношение длин двух струн выражается рациональным числом, хотя и по иной причине. Но если это отношение окажется равно какому-либо нерациональному числу, например, π или квадратному корню из 2, то обертоны двух струн никогда не совпадут точно, хотя частоты более высоких обертонов могут сходиться как угодно близко. Звук, который при этом получается, ужасен.

Так называемая теорема Пифагора – самая знаменитая во всей планиметрии. Хотя ее доказательство приписывают ученикам и последователям Пифагора, например, Архиту Тарентскому, в точности история ее создания неизвестна. Здесь я приведу простейшее доказательство, основанное на понятии пропорциональности, широко применявшемся древнегреческими математиками.

Рассмотрим треугольник с вершинами A, B и P , у которого угол при вершине P является прямым. Теорема утверждает, что площадь квадрата, сторона которого равна AB (гипотенуза треугольника), равняется сумме площадей квадратов, стороны которых равны двум другим сторонам того же треугольника, катетам AP и BP . Говоря языком современной алгебры, рассматривая AB, AP и BP как численные величины, равные длинам указанных сторон, должно быть справедливо равенство:

Чтобы доказать теорему, следует провести перпендикуляр к гипотенузе AB из вершины P . Обозначим точку его пересечения с гипотенузой C (см. рис. 2). Таким образом мы поделим исходный треугольник ABP на два меньших прямоугольных треугольника APC и BPC . Легко видеть, что оба меньших треугольника подобны исходному прямоугольному треугольнику, то есть все углы в них те же самые, что и в большом. Если мы обозначим углы при вершинах A и B α (альфа) и β (бета), то у треугольника ABP будут углы α, β и 90°, и значит, α + β + 90° = 180°. В треугольнике APC два угла равны α и 90°, значит, третий угол равняется β. Аналогично в треугольнике BPC два угла равны β и 90°, следовательно, третий угол равен α.

Так как все три треугольника взаимно подобны, их соответствующие стороны пропорциональны. Это означает, что длина катета AC относится к длине гипотенузы AP треугольника ACP так же, как длина катета AP к длине гипотенузы AB в исходном треугольнике ABP . Соответственно, BC относится к BP в той же пропорции, что и BP к AB . Мы можем выразить это в более привычной алгебраической форме, связав длины сторон пропорцией:

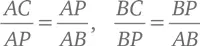
Отсюда очевидно следует, что AP ² = AC × AB , а BP ² = BC × AB . Складывая два этих уравнения вместе, получаем:

Но AC + BC = AB , что и требовалось доказать.

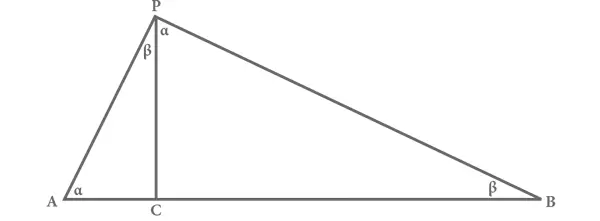
Рис. 2. Доказательство теоремы Пифагора.Согласно теореме, сумма площадей квадратов, стороны которых равны катетам AP и BP , равняется площади квадрата, стороной которого является гипотенуза AB . Для доказательства теоремы из точки P в точку C проводится перпендикуляр к гипотенузе AB .

Математикам Древней Греции были известны лишь рациональные числа. К ним относятся все целые числа, например, 1, 2, 3 и т. д. или целочисленные дроби – 1/2, 2/3 и т. п. Если отношение длин двух отрезков выражалось целочисленной дробью, древнегреческий математик считал, что они «соизмеримы». К примеру, если они находятся в отношении 3/5, это означает, что если один из этих отрезков отложить три раза, а другой пять раз, то получится два отрезка одинаковой длины. Представьте себе потрясение античных математиков, выяснивших, что не все отрезки являются соизмеримыми. Например, в прямоугольном равнобедренном треугольнике гипотенуза несоизмерима ни с одним из двух одинаковых катетов. В понятиях современной математики, поскольку, согласно теореме Пифагора квадрат гипотенузы такого треугольника равен удвоенному квадрату длины любого из катетов, длина гипотенузы равняется произведению длины любого из катетов на квадратный корень из 2. Это означает, что квадратный корень из 2 не является рациональным числом. Доказательство этого факта Евклидом в книге X «Элементов» базируется на первоначальном предположении обратного, что существует рациональное число, квадрат которого равен 2, после чего Евклид опровергает это предположение.

Допустим, что есть рациональное число, выраженное дробью p / q (где p и q – целые числа), чей квадрат равен 2:

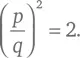
В таком случае будет бесконечное количество таких пар чисел, которые можно получить, умножая p и q на любой натуральный множитель, но предположим, что целые числа p и q – наименьшие целые, для которых верно выражение ( p / q ) 2 = 2. Из уравнения выше следует, что

Отсюда очевидно, что p ² – четное число, но так как произведение двух любых нечетных чисел есть нечетное число, то p должно быть только четным. То есть мы можем записать равенство p = 2 p ', где p ' – целое число. Но тогда

и, повторяя предыдущую цепь рассуждений, находим, что число q также четное и может быть выражено равенством q = 2 q ', где q ' – целое число. Но тогда p / q = p '/ q ', и значит,

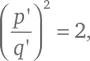
где p ' и q ' – целые числа, которые в два раза меньше p и q соответственно. А это противоречит исходному предположению, что p и q – наименьшие целые числа, для которых равенство ( p / q )² = 2 справедливо. Мы имеем противоречие, и, следовательно, такие числа не могут существовать.

Теорема явным образом обобщается: любое число, например, 3, 5, 6 и т. д., которое само не является квадратом целого числа, не может быть квадратом рационального числа. Например, если 3 = ( p / q )², где p и q – наименьшие целые числа, для которых это равенство справедливо, то p ² = 3 q ², но это невозможно, если только нет такого целого p ', для которого p = 3 p ', но тогда q ² = 3 p '², и q = 3 q ' для некоего целочисленного q ', и, значит, 3 =( p '/ q ')², что противоречит предположению о том, что не существует целых чисел меньше p и q , для которых p 2 = 3 q 2. Поэтому квадратные корни чисел 3, 5, 6, … иррациональны все.