Стивен Вайнберг - Объясняя мир. Истоки современной науки

Чтобы ответить на этот вопрос, Герон предположил, что свет всегда следует кратчайшим путем. В случае отражения это означает, что точка P должна быть расположена так, чтобы общая длина пути из B в P , а затем в A была бы наименьшей среди всех возможных путей из двух прямолинейных отрезков между точкой B , зеркалом и точкой A . Отсюда он заключил, что угол θ п (тета п ) между зеркалом и падающим на него лучом света (отрезком между точкой B и зеркалом) равен углу θ о между зеркалом и отраженным лучом (отрезком между зеркалом и точкой A ).

Доказательство правила о равных углах падения и отражения таково. Начертим прямую, перпендикулярную поверхности зеркала, проходящую через точку B и точку B ′, которая находится на таком же расстоянии позади зеркала, как B перед ним (см. рис. 3). Допустим, что эта прямая пересекает зеркало в точке C . Катеты B ′ C и CP прямоугольного треугольника B ′ CP имеют ту же длину, что и катеты BC и CP в треугольнике BCP , поэтому гипотенузы B ′ P и BP этих двух прямоугольных треугольников также должны быть равны. Значит, полное расстояние, которое луч света проходит из B в P , а потом в A , такое же, как если бы он проходил из B ′ в P , а затем в A . Кратчайшее расстояние между точками B ′ и A – это отрезок прямой, а значит, кратчайший путь между реальным объектом и наблюдателем – такой, при котором точка P лежит на отрезке B ′ A . В случае пересечения двух прямых линий противолежащие по отношению к точке пересечения углы равны, поэтому угол θ между отрезком B ′ P и зеркалом равен углу θ о между отраженным лучом и зеркалом. Но поскольку у прямоугольных треугольников B ′ CP и BCP все стороны одинаковы, угол θ должен быть также равен углу θ п между падающим лучом и зеркалом. Таким образом, поскольку и θ о , и θ п равны θ, они взаимно равны. Это фундаментальное правило равенства углов падения и отражения определяет положение точки P , которая соответствует изображению объекта в зеркале.

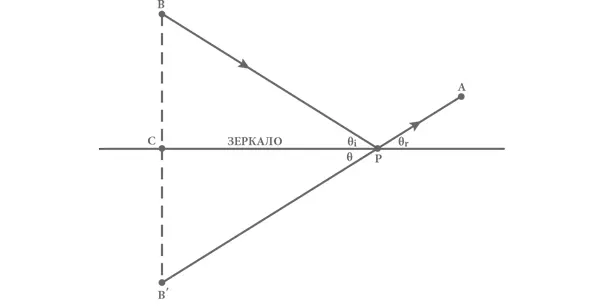
Рис. 3. Доказательство теоремы Герона.Теорема доказывает, что кратчайший путь из объекта B до поверхности зеркала и затем к наблюдателю в точке A таков, что углы θ п и θ о равны. Начерченные сплошной линией отрезки помечены стрелками, показывающими направление движения луча света. Штриховая линия – перпендикуляр к поверхности зеркала между точкам B и B’ , находящимися на одинаковом расстоянии от зеркала, но по разные стороны от него.

В своем великом труде «О плавающих телах» Архимед предположил, что если различные тела плавают или иным образом удерживаются в воде так, что одинаковые сечения на одинаковых глубинах прижимаются вниз различным весом, то и вода, и тела придут в движение и успокоятся тогда, когда все сечения на всех глубинах окажутся придавлены одинаковым весом. Исходя из этого предположения, он сделал несколько общих выводов о поведении плавающих и погруженных тел, некоторые из них даже имели важное практическое значение.

Для начала рассмотрим тело наподобие судна, вес которого меньше веса такого же объема воды. Оно будет плавать на поверхности, вытесняя некоторое количество воды. Если мы выделим в толще воды на какой-то глубине прямо под килем судна горизонтальное пятно такого же размера и формы, как фигура, образуемая ватерлинией судна (где корпус пересекается с поверхностью воды), то вес, приходящийся на площадь этой фигуры, будет равен сумме веса судна и всего объема воды выше этого пятна, за исключением веса воды, вытесненной судном, потому что эта вода больше не находится поверх пятна. Мы можем сравнить этот суммарный вес с тем весом, который действует на такую же площадь, расположенную на той же глубине, но где-либо в стороне от плавающего тела. Разумеется, это значение не будет включать вес плавающего тела, но зато на него будет давить полный вес водяного столба от глубины этого сечения до поверхности, без каких-либо вытесненных частей. Чтобы оба этих сечения испытывали одинаковое давление, вес вытесненной плавающим телом воды должен равняться весу самого плавающего тела. Именно поэтому вес судна называется водоизмещением.

Теперь рассмотрим тело, вес которого больше, чем вес воды такого же объема. Оно не будет плавать, но его можно подвесить в толще воды при помощи веревки или троса. Если конец троса прикрепить к плечу весов, то таким способом мы можем измерить кажущийся вес W каж тела, погруженного в воду. Если мы точно так же, как и в предыдущем случае, выделим в глубине воды прямо под телом равное ему по площади пятно воды, то действующий на него вес будет составлен из двух слагаемых. Первое равно разности истинного веса W ист подвешенного тела и его кажущегося веса W каж , который полностью компенсируется натяжением троса. Второе слагаемое – это вес воды выше пятна, за исключением воды, вытесненной телом. Можно сравнить значение этой суммы с тем весом, который давит на такую же площадь, расположенную на такой же глубине, но в стороне: этот вес не будет включать слагаемые W ист и − W каж , но будет равняться весу столба воды от выделенного сечения до поверхности, без учета какой-либо вытесненной воды. Чтобы на оба сечения действовало одинаковое давление, необходимо выполнение равенства:

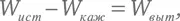
где Wвыт – вес воды, вытесненной подвешенным в воде телом. Взвешивая таким образом тело в воде и вне воды, можно найти W ист и W каж , а отсюда W выт . Если объем тела равен V , то

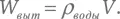
Здесь ρ воды (ро) обозначается плотность (отношение веса к объему) воды, это значение приблизительно равняется 1 г/см³. (Конечно, для тела простой формы, например куба, его объем можно определить простым обмером, но это трудно сделать для тела неправильной формы вроде короны.) Кроме того,

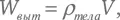
где ρ тела – плотность тела. Если взять отношение W ист к W выт , то объем V сократится в дроби, и, таким образом, измеряя W каж и W ист , мы можем определить отношение плотностей тела и воды:

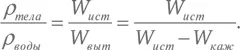
Полученная величина называется относительной плотностью материала, из которого изготовлено тело. Например, если в воде тело весит в воде на 20 % меньше, чем в воздухе, то W ист− W каж = 0,20 × W ист , то есть его плотность должна быть в 1/0,2 = 5 раз больше плотности воды. Иными словами, его относительная плотность по отношению к воде равняется 5.