Ричард Фейнман - Характер физических законов

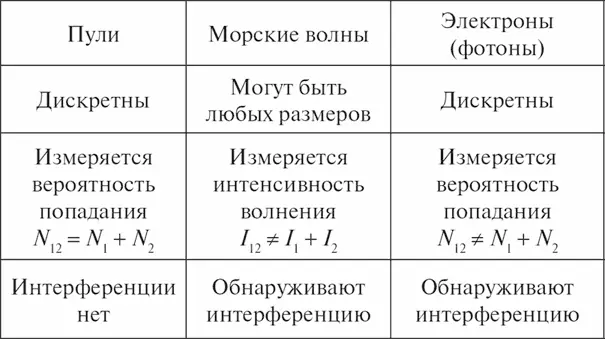
Теперь подведем итог. Итак, электроны попадают в детектор дискретными порциями, как если бы это были частицы, но вероятность попадания этих частиц определяется по тем же законам, по каким определяется интенсивность волнения воды. Именно в этом смысле можно говорить, что с одной точки зрения электрон ведет себя как частица, а с другой – как волна. Он ухитряется одновременно быть двумя совершенно разными понятиями (см. табл. 2).

Вот и все, что можно сказать по этому поводу.

Я мог бы привести сейчас математическое описание того, как вычислять вероятность попадания электрона при произвольных обстоятельствах, и в принципе на этом можно было бы закончить лекцию. Но в том, что природа ведет себя именно так, а не иначе, есть несколько тонкостей. Мы сталкиваемся с целым рядом непонятных явлений, и именно о них мне и хотелось бы поговорить сейчас, поскольку они не вытекают сразу же из того, что рассказано мной выше.

Таблица 2

Начнем с одного утверждения, казалось бы разумного, поскольку мы установили дискретный характер электронов или фотонов. Так как в детектор приходит нечто целое (электрон в нашем примере), по-видимому, разумно предположить, что электрон попадает в детектор либо через отверстие 1 , либо через отверстие 2 . Кажется очевидным, что, так как электрон нечто целое и неделимое, ничего другого и не может быть. Назовем это утверждение утверждением А.

Электрон попадает в детектор

либо через отверстие 1 ,

либо через отверстие 2 .

На самом деле мы уже немного говорили о том, что происходит с утверждением А. Если бы было верно, что электрон попадает в детектор либо через отверстие 1 , либо через отверстие 2 , то общее число зарегистрированных электронов должно было бы распадаться на сумму электронов двух типов. Общее число этих электронов было бы суммой числа электронов, прилетевших через первое отверстие, и числа электронов, прилетевших через второе. Но так как суммарную кривую не удается представить таким удобным образом в виде суммы двух других кривых и поскольку эксперимент, позволяющий регистрировать прилетающие электроны в случае, когда открыто только одно отверстие, показывает, что в случае двух отверстий мы не наблюдаем суммы двух вероятностей появления, приходится заключить, что это утверждение неверно. Но если неверно, что электрон попадает в детектор либо через отверстие 1 , либо через отверстие 2 , может быть, он временно распадается на две половины или что-нибудь в этом роде. Итак, утверждение А ложно. Такова логика. К сожалению или нет, но логику можно проверять экспериментально. Теперь нам нужно решить, что же происходит на самом деле. Попадает ли электрон в детектор либо через отверстие 1 , либо через отверстие 2 , или, может быть, он успевает проскочить каждое из отверстий по нескольку раз в разных направлениях, или расщепляется временно на две части, или что-нибудь другое в этом же духе.

Нам нужно всего лишь понаблюдать за поведением электронов. А для этого нам нужен свет. Поэтому за отверстиями мы и поместим очень мощный источник света. Электроны рассеивают свет, который отражается от них, и, если свет достаточно силен, вы сможете заметить пролетающие электроны. Отойдем теперь назад и попытаемся увидеть, что происходит в момент регистрации электрона или на какую-то долю секунды до этого. Наблюдается ли вспышка за отверстием 1 или 2 , или, быть может, так сказать, по полвспышки за каждым из этих отверстий? Ведь это позволит нам, наблюдая, найти, что же происходит в самом деле. Итак, включим свет, начнем наблюдать, и вот тебе на – каждый раз перед щелчком нашего детектора вспыхивает только одно отверстие – либо 1 , либо 2 . Оказывается, всегда, абсолютно во всех случаях, электрон, когда мы за ним наблюдаем, попадает в детектор либо через отверстие 1 , либо через отверстие 2 . Парадокс!

Постараемся теперь загнать природу в угол. Сейчас я вам расскажу, что для этого нужно сделать. Мы оставим наш источник света включенным и станем одновременно и наблюдать за вспышками, и считать число пролетающих электронов. Из результатов этих наблюдений составим два столбца: один – в котором мы станем отмечать электроны, пролетевшие через отверстие 1 , и другой – регистрирующий электроны, пролетевшие через отверстие 2 , а по мере того как будет щелкать наш детектор, станем отмечать в этих столбцах, какой из электронов попал в него. Так как же будет выглядеть столбец 1 , после того как я сложу все результаты, соответствующие одному и тому же положению детектора? Что я увижу, если я наблюдаю лишь за отверстием 1 ? Я получу кривую N 1(рис. 32). Этот столбец оказывается распределенным точно так же, как если бы мы считали, что второе отверстие закрыто. Здесь ничего не меняется от того, наблюдаем мы за полетом электронов или нет. Если мы закроем отверстие 2 , получим то же распределение прилетающих электронов, какое мы получаем, оставляя его открытым и наблюдая за отверстием 1 . То же самое получается в результате наблюдения за отверстием 2 ; на этот раз получается кривая N 2. Но, послушайте, суммарное число зарегистрированных детектором электронов должно быть суммой. Оно должно равняться сумме числа N 1и числа N 2, так как относительно каждого из пролетевших отверстия электронов известно, какому, первому или второму, столбцу он принадлежит. Суммарное число зарегистрированных электронов просто не может быть ничем другим , кроме суммы этих двух чисел. Оно должно распределяться как N 1+ N 2. Но ведь мы говорили, что оно распределено как N 12. Нет, оно распределено как N 1+ N 2. Конечно, на самом деле так оно и есть. Так должно быть, и так оно и есть. Если мы пометим штрихом величины, относящиеся к опыту с зажженным светом, то окажется, что практически не отличается от N 1для опыта без источника света, a очень мало отличается от N 2. Но число, наблюдаемое в случае, когда свет горит и оба отверстия открыты, равно сумме числа частиц, которые мы видели пролетающими через отверстие 1 , и числа электронов, пролетевших, как мы видели, через отверстие 2 . Вот к какому результату мы приходим, включив свет. Значит, в зависимости от того, включим мы свет или нет, мы получим разные результаты. Зажжем свет, и распределение будет описываться кривой N 1+ N 2. Выключим свет, и распределение сразу примет вид N 12. Включим его снова, и снова получим N 1+ N 2. Вы видите, природа опять вывернулась! Приходится говорить, что свет влияет на результат. Если свет включен, то вы получите другой результат, чем если бы он был выключен. Вы можете еще сказать, что свет влияет на поведение электронов. Если мы станем говорить об экспериментальном исследовании движения электронов, что не совсем точно сказано, то можно утверждать, что свет влияет на это движение, в результате чего электроны, которые сами по себе попали бы в верхнюю часть последнего экрана, отклоняются, так сказать, сбиваются со своей траектории и попадают в нижнюю часть, сглаживая распределение таким образом, что в результате получается просто-напросто сумма N 1+ N 2.