Елена Замедлина - Статистика. Шпаргалка

Группировка является важнейшим этапом статистического исследования, соединяющим сбор первичной информации об объекте исследования и анализ этой информации на основе обобщающих статистических показателей.

Основные задачи,которые решаются с помощью группировок:

1) выделение социально-экономических типов;

2) изучение структуры социально-экономических явлений;

3) выявление связи между явлениями.

При проектировании группировок возникают следующие важнейшие проблемы:

1) определение группировочного признака (основания группировки). Группировочный признак– признак, по которому происходит включение единиц в группы. Его выбор зависит от цели группировки и сущности данного явления;

2) выделение числа групп. Число групп определяется с таким расчетом, чтобы в каждую группу попало достаточно большое число единиц;

3) определение интервалов групп. Интервалы могут быть равными и неравными. Последние, в свою очередь, делятся на равномерно возрастающие и равномерно убывающие.

В зависимости от круга решаемых задач выделяют следующие виды группировок:

1) типологические группировки.Их задача – классификация социально-экономических явлений путем выделения однородных в качественном отношении групп;

2) структурные группировки.Их задача – изучение состава отдельных типических групп при помощи объединения единиц совокупности, близких друг к другу по величине группировочного признака;

3) аналитические группировки.Их задача– выявление связи между социально-экономическими явлениями путем оценки влияния одних признаков на другие. В основе аналитической группировки лежит признак-фактор, влияние которого на результативные признаки изучается.

Группировка, в которой группы образованы по одному признаку, называется простой.Если для характеристики явления недостаточно разбить совокупность на группы по какому-либо однородному признаку, строят сложные группировки.

Сложнойназывается группировка, в которой разделение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации). Такие группировки дают возможность изучить структуру совокупности по нескольким признакам одновременно.

Социально-экономический анализ предполагает использование системы простых и комбинационных группировок.

Также часто прибегают к вторичной группировке-перегруппировке уже сгруппированных данных. Вторичная группировка может быть проведена методом простого укрупнения интервала.

Социально-экономические явления и процессы характеризуются статистическими показателями. Все экономические и социальные категории или понятия носят абстрактный характер, отражают наиболее существенные черты, общие взаимосвязи явлений. Для того чтобы измерить размеры и соотношения явлений или процессов, дать им соответствующую количественную характеристику, разрабатывают экономические и социальные показатели, соответствующие каждой категории.

Статистические показатели разрабатываются в соответствии с научной методологией. Каждый статистический показатель имеет качественное социально-экономическое содержание и связанную с ним методологию измерения. У статистического показателя имеются следующие формы выражения:

1) общее число единиц совокупности;

2) общая сумма значений количественного признака единиц совокупности;

3) средняя величина признака;

4) величина данного признака по отношению к величине другого.

Статистический показатель имеет определенное количественное или числовое значение, выраженное в определенных единицах измерения, которое называется его величиной.

Статистические показатели можно условно подразделить на первичные и вторичные. Первичныехарактеризуют либо общее число единиц совокупности, либо сумму значений какого-либо их признака. По статистической форме эти показатели являются суммарными статистическими величинами.

Вторичные(производные) показатели обычно выражаются средними и относительными величинами.

Показатели, характеризующие размер сложного комплекса социально-экономических явлений и процессов, называют синтетическими(ВВП, национальный доход, производительность общественного труда, потребительская корзина и др.).

В зависимости от применяемых единиц измерения различают показатели натуральные, стоимостные и трудовые. В зависимости от сферы применения различают показатели, исчисленные на региональном, отраслевом и прочих уровнях. Поточности отражаемого явления различают ожидаемые, предварительные и окончательные величины показателей.

Все статистические показатели по охвату единиц совокупности делятся на индивидуальные и сводные. Индивидуальные показателихарактеризуют отдельные единицы совокупности. Сводные показателихарактеризуют группу единиц совокупности или всю совокупность в целом.

Объективное и достоверное исследование сложных экономических и социальных категорий возможно только на основе системы статистических показателей. Система статистических показателей– это совокупность взаимосвязанных статистических показателей, имеющая одноуровневую и многоуровневую структуру и нацеленная на решение конкретной статистической задачи.

Средняя величина– обобщающий показатель, в котором находят выражение действия общих условий, закономерностей изучаемого явления.

Средние величины тесно связаны с законом больших чисел.

С помощью метода средних величин решаются следующие основные задачи:

1) характеристика уровня развития явлений;

2) сравнение двух или нескольких уровней;

3) изучение взаимосвязей и явлений;

4) анализ размещения явлений в пространстве.

Для решения этих задач используются следующие виды средних величин.

1. Средняя арифметическая (простая)– сумма всех значений варьирующего признака, поделенная на количество единиц совокупности:

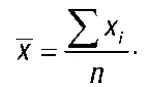
2. Средняя арифметическая (взвешенная). Применяется, когда известны отдельные значения признака и их веса ( f i ):

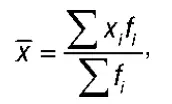
где x i – варианты осредняемого признака;

f i – частота, которая показывает, сколько раз встречается i- е значение в совокупности.