Елена Замедлина - Статистика. Шпаргалка

В качестве нижней границы второго интервала принимается верхняя граница первого, а верхнюю границу второго интервала получают прибавлением к верхней границе шага h. Процедуру повторяют до тех пор, пока не будут определены границы последней группы;

4) разносят единицы совокупности по интервалам;

5) подсчитывают единицы совокупности в каждом интервале.

Если полученные указанными выше способами группировки не удовлетворяют требованиям анализа, то производят перегруппировку. Ряды распределения используются в статистике как средство систематизации и упорядочивания материалов наблюдения, как метод изучения структуры явлений, анализа самих распределений и вариативности группировочного признака.

Табличное распределение частот вариационного ряда обычно дополняют его графическим представлением. Схематически все множество графических представлений статистических данных разделяют на два класса: диаграммы и линейные изображения. К классу линейных графиков относятся полигон распределения, кумулятивная кривая, кривая концентрации, огива. К классу диаграмм относится гистограмма.

Вариационные ряды могут изображаться графически путем построения полигона распределения, гистограммы, кумуляты.

Для графического изображения дискретного вариационного ряда строится x min полигон распределенияx minв прямоугольной системе координат. На оси абсцисс проставляются варианты, на оси ординат – частоты. На пересечении каждой абсциссы и ординаты строятся точки, которые затем соединяются отрезками прямой. Крайние точки соединяются с осью абсцисс в точках, отстоящих от минимального и максимального варианта на одно деление. Полигоном частотназывают ломаную, отрезки которой соединяют точки (x 1, f 1, …,(x nf n). Иногда крайние точки соединяют с точками, имеющими нулевую ординату. Полигоном относительных частотназывают ломаную, отрезки которой соединяют точки ( x 1, w 1), …, ( x n , w n ), где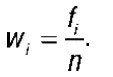

Интервальные вариационные ряды изображаются в виде гистограммы.На оси абсцисс откладываются отрезки, соответствующие длине интервала h. На каждом отрезке строятся прямоугольники, одна сторона каждого из них лежит на оси абсцисс, длина второй стороны соответствует частоте f i или плотности 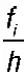. Гистограммой частотназывают ступенчатую фигуру, состоящую из полученных прямоугольников. Гистограммой относительных частотназывают ступенчатую фигуру, состоящую из прямоугольников, основаниями которых случат интервалы длиной h, а высоты которых равны .

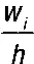Любой вариационный ряд можно изобразить графически в виде кривой накопленных частот – кумуляты.На оси абсцисс откладываются либо варианты, либо границы интервалов. Наоси ординат– накопленная частота. Получают точки при пересечении каждой пары абсциссы и ординаты, которые соединяют плавной кривой.

Кумулятивная кривая (кривая сумм)– ломаная, составленная по последовательно суммированным, т.е. накопленным частотам или относительным частотам. При построении кумулятивной кривой дискретного признака на ось абсцисс наносятся значения признака, а ординатами служат нарастающие итоги частот. Соединением вершин ординат прямыми линиями получают кумуляту. При построении кумуляты интервального признака на ось абсцисс откладываются границы интервалов и верхним значениям присваивают накопленные частоты. Кумулятивную кривую называют полигоном накопленных частот.

Если на ось ординат нанести значение признака, а на ось абсцисс – накопленные частоты, то получим кривую, называемую огивой.

Вариацией признаканазывается различие индивидуальных значений признака внутри изучаемой совокупности. Вариация возникает в результа-те того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но не показывает строения совокупности, которое весьма существенно для ее познания.

Размах вариации– разность между наибольшим х maxи наименьшим х minзначениями вариантов изучаемого признака: R = x max– x min.

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение 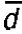, которое учитывает различие всех единиц изучаемой совокупности.

Среднее линейное отклонениеопределяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:

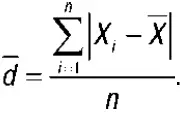
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:

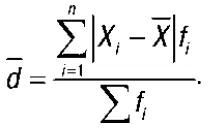
Дисперсия– это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается σ 2. В зависимости от исходных данных дисперсия может вычисляться по простой или взвешенной средней арифметической:

1) 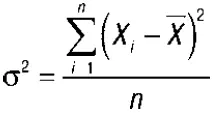– дисперсия невзвешенная (простая);

2) 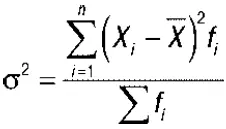– дисперсия взвешенная.

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается о. Вычисляется оно следующим образом:

1) 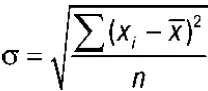– среднее квадратическое отклонение (невзвешенное);

2) 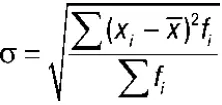– среднее квадратическое отклонение (взвешенное).

Статистическое наблюдение– массовое, планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, которое заключается в регистрации отобранных признаков у каждой единицы совокупности.