Елена Замедлина - Статистика. Шпаргалка

Для дискретного вариационного ряда значения вариантов умножают на соответствующие частоты и сумму этих произведений делят на сумму частот.

Для интервального вариационного ряда находится среднее значение интервала для каждой группы как полусуммы его верхней и нижней границ.

3. Средняя хронологическаяприменяется для моментного ряда с равными интервалами между датами:

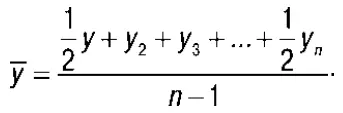
4. Средняя гармоническая (простая)применяется, когда веса всех вариантов (f) равны:

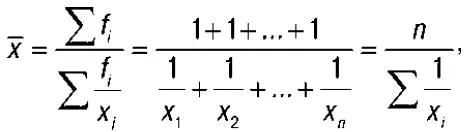
где х i – отдельные варианты;

п — число вариантов осредняемого признака.

5. Средняя гармоническая (взвешенная):

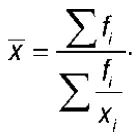
В статистике используются различные формы(виды) средней величины, которые могут быть представлены в виде общей формулы:

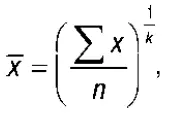
где 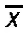– средняя величина;

х— индивидуальное значение;

п — число единиц изучаемой совокупности;

к — показатель степени, определяющий вид средней.

Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.

Ряды распределения представляют собой группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе л ибо удельный вес этой численности в общем итоге. В зависимости от признака, положенного в основу ряда распределения, различают атрибутивные и вариационные ряды распределения.

Атрибутивныминазывают ряды распределения, построенные по качественным признакам. Ряды распределения принято оформлять в виде таблиц. Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Данные, взятые за несколько периодов, позволяют исследовать изменение структуры явления или процесса.

Вариационныминазывают ряды распределения, построенные по количественному признаку. Вариационный ряд распределения может быть построен по непрерывно варьирующемупризнаку (когда признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующемупризнаку (когда признак принимает строго определенные целочисленные значения). Построение непрерывного (интервального) вариационного ряда основано на принципах статистической группировки.

Любой вариационный ряд состоит из элементов: вариантов и частот. Вариантамисчитаются отдельные значения признака, которые он принимает в вариационном ряду, т.е. конкретны значения варьирующего признака. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными. Частоты– это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Обозначаются они f i Сумма всех частот определяет численность всей совокупности, ее объем:

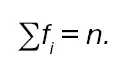
Численности групп, выраженные в процентных долях единицы, называются частостями и обозначаются w i Сумма частостей равна 1, если они выражены в долях единицы, и 100 %, если они выражены в процентах.

В непрерывном вариационном ряду с равными интервалами частоты показывают степень заполнения интервала единицами совокупности. При неравных интервалах частоты не характеризуют степень их заполнения. В этом случае рассчитывается плотность распределения.Этот показатель определяется числом единиц совокупности, приходящимся в среднем на одну единицу ширины интервала. Абсолютная плотность распределенияопределяется отношением частоты на ширину интервала, относительная плотность распределения –отношением частости к ширине интервала.

Для атрибутивных и вариационных рядов применяют различные способы построения.

1. Построение атрибутивных рядов распределения.Атрибутивные ряды распределения обычно представляются в форме таблицы, причем в подлежащем такой таблицы перечисляются варианты атрибутивного признака, по которому строится ряд распределения. Как правило, число таких вариантов конечно. Если вариантов слишком много, то можно объединить некоторые из них (сущностно подобные) в классы, которые и будут новыми вариантами атрибутивного признака. В сказуемом таблицы отражаются частоты или частости каждого варианта, либо накопленные частоты или накопленные частости. Ряды распределения могут строиться по накопленным частотам,которые показывают, какое количество единиц имеет величину варианта не больше данной. Если вместо абсолютных частот взять частости, то аналогично получают и накопленные частости.

2. Построение дискретных вариационных рядовпроизводится в следующей последовательности:

1) располагают варианты изучаемого признака в ранжированном порядке;

2) производят разноску единиц совокупности по вариантам (группировкам). Для этого строят таблицу;

3) подсчитывают количество единиц в каждой группе, т.е. определяют частоту каждого варианта. Частоты можно заменять частостями или использовать накопленные частоты (частости).

3. Построение интервального вариационного рядапроизводится в следующей последовательности:

1) выбирают оптимальное число групп (интервалов признака), на которые следует разбить совокупность. Число групп выбирается так, чтобы отразить многообразие значений признака в совокупности. Число групп устанавливается по формуле: к= 1 + 3,32lg N = 1 ,44 × ln N+ 1 (формула Стерджесса), где к– число групп; N — численность совокупности;

2) устанавливают длину интервала (шаг), которую рассчитывают по формуле:

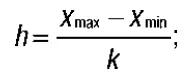
3) определяют границы всех интервалов. Нижняя граница первого интервала принимается за х min, верхняя граница первого интервала находится по формуле: x min+ h.