Аурика Луковкина - Техническая механика. Шпаргалка
- Название:Техническая механика. Шпаргалка
- Автор:
- Жанр:
- Издательство:Array Литагент «Научная книга»
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Аурика Луковкина - Техническая механика. Шпаргалка краткое содержание
Техническая механика. Шпаргалка - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Численно равнодействующая равна главному вектору системы сил, но приложена к другой точке, относительно которой главный момент равен нулю. Равнодействующая обозначается F Σ.
Численно ее значение определяется так же, как главный вектор системы сил.
Возможно несколько вариантов при приведении системы сил к точке.
1. F ГЛ = 0
М ГЛ 0≠ 0 →тело вращается вокруг неподвижной оси.
2. М ГЛ = 0
F ГЛ 0≠ 0; F ГЛ = F Σ →тело движется прямолинейно ускоренно.
3. M ГЛ = 0
F ГЛ 0 = 0 →тело находится в равновесии.
7. Балочные системы
Балка– это конструктивная деталь в виде прямого бруса, закрепленного на опорах, и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с ее длиной.
Виды нагрузок.По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузка называется сосредоточенной.
Если нагрузка распределена по значительной площадке или линии (давление воды на плотину, снега на крышу и т. д.), то она является распределенной.
Жесткая заделка (защемление).Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы R Ах и R Ау и парой моментов М R .
Шарнирно-подвижная опора.Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности.
Шарнирно-неподвижная опора.Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Неизвестны три силы, две из них – вертикальные, следовательно, для определения неизвестных следует использовать систему уравнений во второй форме:
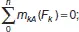 (1)
(1)
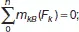 (2)
(2)
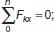 (3)
(3)
Составляются уравнения моментов относительно точки крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении остается одна неизвестная сила.
Из уравнения (3) определяется реакция R Вх .
Из уравнения (1) определяется реакция R Ву .
Из уравнения (2) определяется реакция R Ау .
Для контроля правильности решения используется дополнительное уравнение:
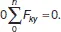
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, используется система уравнений в третьей форме.
8. Пространственная сходящаяся система сил
Момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
M 00( F ) = npFa,
где а – расстояние от оси до проекции F ;
прF – проекция силы на плоскость, перпендикулярную оси 00.
Момент считается положительным, если сила разворачивает тело по часовой стрелке (смотреть со стороны положительного направления оси).
Если линия действия силы пересекает ось или линия действия силы параллельна оси, моменты силы относительно этой оси равны нулю.
Силы и ось лежат в одной плоскости, они не могут повернуть тело вокруг оси.
Вектор в пространстве. В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора образуют ребра прямоугольного параллелепипеда, вектор силы совпадает с диагональю.
Модуль вектора определяется из формулы:
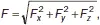
где F x = F cosα x ;
F y= F cosα y ;
F z = F cosα z ;
α x, α y, α z – угол между вектором F и осями координат.
Пространственная сходящаяся система сил – это система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник:
F Σ = F 1 + F 2 + F 3 + … + F n .
Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Модуль равнодействующей можно определить аналитически, используя метод проекций – совмещая начало координат с точкой пересечения линий действия сил системы, и, проецируя все силы на оси координат. Суммируем соответствующие проекции, получаем проекции равнодействующей на оси координат.
Модуль равнодействующей системы сходящихся сил:
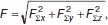
Направление вектора равнодействующей определяется углами.
9. Центр тяжести
Сила тяжести – равнодействующаясил, она распределена по всему объему тела.
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) применим теорему Вариньона о моменте равнодействующей:
«Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно любой точки».
Тело состоит из нескольких частей, силы тяжести которых g k приложены в центрах тяжести (ЦТ) этих частей.
Равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре G .
х С , у С и z С – координаты центра тяжести G .
х k , у k и z k – координаты центров тяжести частей тела.
Из теоремы Вариньона следует:
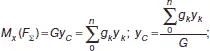
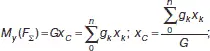
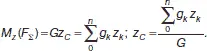
В однородном теле сила тяжести пропорциональна объему V:
G = γV,
где g – вес единицы объема.
Для однородных тел:
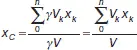
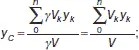
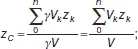
где V k – объем элемента тела;
V – объем всего тела.
Выражение
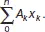
называется статическим моментом площади ( S y ).
10. Основные понятия кинематики
Основные кинематические параметры.
Читать дальшеИнтервал:
Закладка:










