Аурика Луковкина - Радиотехника. Шпаргалка
- Название:Радиотехника. Шпаргалка
- Автор:
- Жанр:
- Издательство:Array Литагент «Научная книга»
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Аурика Луковкина - Радиотехника. Шпаргалка краткое содержание
Радиотехника. Шпаргалка - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
В нелинейной системе принцип суперпозиции не выполняется, что с математической точки зрения обусловлено нелинейностью уравнений, описывающих систему.
9. Свободные колебания в LC-контуре
Простой и широко используемой в радиотехнике линейной системой с постоянными параметрами является колебательный контур, содержащий конденсатор C , катушку индуктивности L и сопротивление R . Пусть в момент времени t = 0 на конденсаторе имеется заряд q 0= CU 0. Закон изменения заряда на конденсаторе найдем на основе закона Кирхгофа:
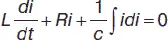 (14)
(14)
Учитывая, что 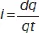 и вводя обозначение
и вводя обозначение 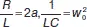 ( a коэффициент затухания, ω – собственная частота контура), представим (14) в виде
( a коэффициент затухания, ω – собственная частота контура), представим (14) в виде
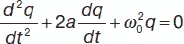 (15)
(15)
Аналогичные уравнения получаются для напряжений на элементах L и C и для силы тока в контуре. Если ω 0 2>> α 2, решение уравнения (15) записывается в виде:
q = q me - at cos( ωt + φ ), (16)
где 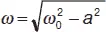 .
.
Таким образом, при ω 0 2>> а 2зависимость заряда на конденсаторе от времени имеет характер затухающего колебания, частота которых ω , называемая частотой свободных колебаний, несколько меньше собственной частоты контура ω 0. Ток в контуре также совершает затухающие колебания:
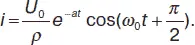
Начальная амплитуда колебаний:
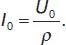
Важным параметром колебательного контура является добротность Q, характеризующая относительное уменьшение энергии в процессе колебаний:
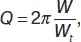 (17)
(17)
где W запасенная энергия,
W t– энергия, теряемая за период.
В цепях постоянного тока существует лишь механизм потери энергии. Это потери на нагревание проводников, определяемые законом Джоуля – Ленца:
P Ом= I 2 R Ом,
где 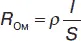 – омическое сопротивление.
– омическое сопротивление.
Связанные с R Омпотери энергии называют омическими потерями. В цепях переменного тока, особенно при высокой частоте колебаний, появляются дополнительные механизмы потери энергии, потери на излучение потери в диэлектрике конденсаторов, потери, связанные с токами Фукои гистерезисом (если катушки индуктивности имеют ферромагнитные сердечники) и др.
Добротность контура определяется по формуле:
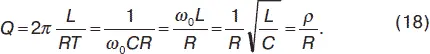
10. Вынужденные колебания в последовательном контуре
Контур подключен к источнику внешней гармонической электродвижущей силы с амплитудой ξ m и начальной фазой φ е (рис. 3).
e = ξ m cos( ω ) t + φ e ) (19)
В соответствии с законом Кирхгофа получаем:
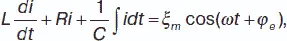 (20)
(20)
где 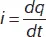 .
.
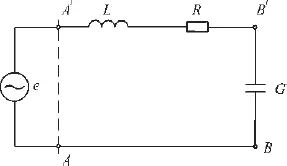
Рис. 3
При нахождении амплитуды и начальной фазы вынужденных колебаний пользуются методом комплексных амплитуд.
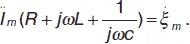 (21)
(21)
Комплексную величину
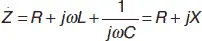
называют полным сопротивлением или импендансомпоследовательного контура;
где R – активное,
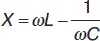 – реактивное сопротивление контура.
– реактивное сопротивление контура.
Из условия равенства нулю реактивного сопротивления определяется резонансная частота контура:
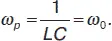
При частоте ЭДС меньше резонансной реактивное сопротивление отрицательно и бесконечно возрастает при w → 0, т. е. при Х > 0 и бесконечно возрастает при ω → ω 0, последовательный контур эквивалентен индуктивности L экв. Поведение сложных цепей описывают с помощью понятий эквивалентного сопротивления, эквивалентной емкости, эквивалентной индуктивности.
К комплексным амплитудам применимы правила Кирхгофа. При последовательном соединении элементов, складываются импендансы, при параллельном – обратные величины.
i = I me jωt
где I m– комплексная амплитуда силы тока в контуре.
Воспользовавшись показательной формой представления комплексных чисел, получим:
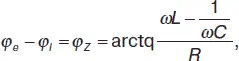 (24)
(24)
откуда I me jφ IZe jφ z = ξe jφ e .
При ω = ω 0, х = 0 из следует, что при резонансе φ I φ e = 0, т. е. отсутствует сдвиг фаз между ЭДС и током.
11. Линейный четырехполюсник. Характеристики четырехполюсника
Задачей линейных цепей является передача и фильтрация сигналов в тракте канала радиосвязи.
Радиотехническую цепь, через которую проходит сигнал, часто можно представить в виде четырехполюсника – устройства, имеющего два входных и два выходных зажима.
Если четырехполюсник представляет собой линейную цепь с постоянными параметрами то при подаче на его вход синусоидального сигнала U вхc некоторой амплитудой, частотой и фазой на выходе появится также синусоидальный сигнал U выхтой же частоты, однако амплитуда и фаза могут быть иными. При прохождении сигнала через линейный четырехполюсник с постоянными параметрами изменяется его комплексная амплитуда.
Линейный четырехполюсник характеризуется комплексным коэффициентом передачи:
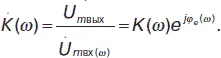 (25)
(25)
Модуль коэффициента передачи К ( ω ) дает отношение действительных амплитуд выходного и входного напряжений, а аргумент ( φ к ( ω ) – изменение начальной фазы выходного напряжения по сравнению с входным.
Читать дальшеИнтервал:
Закладка:










