Аурика Луковкина - Радиотехника. Шпаргалка

Пусть требуется обеспечить неискаженную передачу сигнала U вх( t ) через некоторый четырехполюсник Сигнал на выходе будет иметь вид:

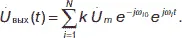(26)

В идеальном случае при прохождении через четырехполюсник все спектральные составляющие входного сигнала должны изменяться по амплитуде в одинаковое число раз k и испытывать одинаковое запаздывание t 0во времени. Для неискаженного воспроизведения сигнала комплексный коэффициент передачи четырехполюсника должен иметь вид:

К ( ω ) = Кe - ω t 0 , (27)

т. е. его модуль должен быть одинаковым для всех передаваемых частот ( К ( ω ) = const), а аргумент – представлять собой линейную функцию частоты ( φk ( ω ) = – ωХ 0). Зависимость модуля коэффициента передачи от частоты называют амплитудно-частотной (или просто частотной) характеристикой, а от фазы – фазочастотной (или фазовой) характеристикой.

Наряду с требованиями, предъявляемыми к четырехполюсникам в отношении идеальной передачи полезных сигналов с некоторой шириной спектра Δ ω сигн,необходимо, чтобы коэффициент передачи четырехполюсника вне желаемой частоты обращался в нуль так как любые сигналы, спектр которых находится вне полосы частот полезного сигнала, являются помехами. Идеальный четырехполюсник должен иметь п-образную частотную характеристику.

У реального четырехполюсника форма характеристики отличается от п-образной. Это приводит к искажению сигнала – тем большему, чем сильнее это отличие. Допустимые искажения сигнала и требования к характеристикам K ( ω ) и φ К( ω ) зависят от конкретной системы передачи сигнала. В тракте радиовещательного приемника удовлетворительными принято считать четырехполюсники, для которых в рабочей полосе частот коэффициент передачи меняется менее чем в 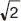раз.

Последовательный контур изображенный на рис. 4 – пример линейного четырехполюсника, который можно использовать в качестве фильтра.

Рис. 4

Входными зажимами фильтра являются зажимы АА' , выходными – ВВ' . Коэффициент передачи такого фильтра:

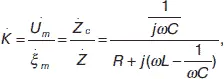
где R – активное сопротивление контура (сопротивление источника ЭДС не учитывается).

Представим числитель и знаменатель в показательной форме:

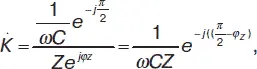
откуда модуль и аргумент коэффициента передачи соответственно имеют вид:

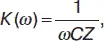(29)

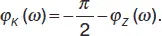(30)

Выражение – это амплитудно-частотная, а (30) – фазочастотная характеристика фильтра.

Полосу пропусканияфильтра определяют из условия, что на границе полосы модуль коэффициента передачи фильтров уменьшается в 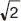раз по сравнению с его значением при резонансе, т. е. при ξ = 0. Уравнение для определения полосы пропускания последовательного контура имеет вид:

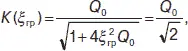(31)

где ξ – расстройка, соответствующая граничным частотам фильтра.

Из (31) получим выражение для относительной ξ ппропи абсолютной Δ f пропполосы пропускания фильтра:

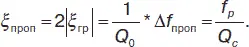(32)

При рассмотрении фильтрующих свойств последовательного контура мы пренебрегли внутренним сопротивлением источника ЭДС. В реальной ситуации любой источник сигнала характеризуется некоторой ЭДС и внутренним сопротивлением R . Если источник включается в последовательный контур, полное активное сопротивление контура становится равным R + R гс учетом R г, добротность последовательного контура

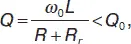
где 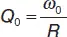– собственная добротность контура.

Из-за больших потерь энергии, возникающих на внутреннем сопротивлении генератора, значительно уменьшается добротность контура, и расширяется полоса пропускания фильтра.

Рассмотрим фильтрацию радиосигнала в схеме с параллельным контуром (рис. 5). Импенданс этого контура Z К . Коэффициент передачи четырехполюсника, имеющего входные зажимы АА' , выходные ВВ' :

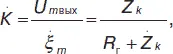(34)

где ξ m, U m – комплексные амплитуды ЭДС и напряжения на контуре соответственно.

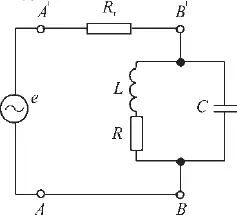
Рис. 5

Для нахождения K надо предварительно найти импенданс параллельного контура:

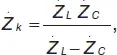(35)

где 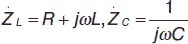– импендансы двух параллельных ветвей.

Подставив Z Lи Z Cв (35), получим:

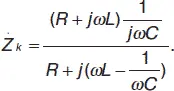(36)

В наиболее интересном с практической точки зрения случае, когда частота «близка» к резонансной частоте

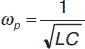
контура, выражение (36) можно упростить.

Знаменатель (36) равен импендансу Z последовательного контура, который имеет вид:

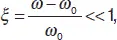
Полоса пропускания:

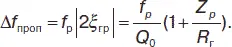(37)

Эта полоса тем ближе к собственной полосе контура

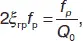
чем меньше отношение .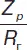

При R → 0 полоса пропускания неограниченно возрастает, а контур полностью утрачивает избирательные свойства. При использовании контура – фильтра в радиоустройствах необходимо учитывать влияние на его избирательные свойства не только внутреннего сопротивления источника сигнала, но также сопротивления цепей, являющихся нагрузкой фильтра.