Владимир Живетин - Безопасность полета вертолета. Системы аэромеханического контроля

В главе разрабатываются аэромеханические методы измерения пилотажных параметров движения вертолета на основе информации о поле аэродинамических давлений в характерных точках лопасти несущего винта (НВ) вертолета.

В первом разделе рассматривается вопрос об использовании информации о величине среднего квадрата пульсаций перепада давления в определенной точке лопасти с целью идентификации продольной скорости движения несущего винта. Проведена оценка погрешности предлагаемого способа измерения продольной скорости движения НВ.

Второй раздел посвящен вопросу совместной идентификации полной аэродинамической силы НВ, его продольной и осевой скоростей движения на основе информации о величинах перепадов давления в двух различных сечениях лопасти и информации о величине среднего квадрата пульсаций перепада давления в заданной точке лопасти. Проведена оценка погрешности метода совместного измерения указанных выше параметров движения НВ вертолета.

Как известно, на режимах висения и осевом движении НВ отсутствует циклический шаг лопастей и аэродинамическая нагрузка на лопасти не изменяется при ее вращении. При наличии продольной составляющей скорости движения НВ для выравнивания моментов сил относительно продольной оси с помощью автомата перекоса задается циклический шаг лопастей. И наличие продольной составляющей скорости движения НВ, и циклический шаг лопастей, и неравномерность поля индуктивных скоростей в плоскости диска НВ при полете вперед вызывают пульсацию аэродинамической нагрузки на лопасти при ее вращении. При этом, как показывают теоретические и экспериментальные исследования (рис. 5.l), с увеличением продольной скорости движения НВ пульсации аэродинамической нагрузки на лопасти возрастают.

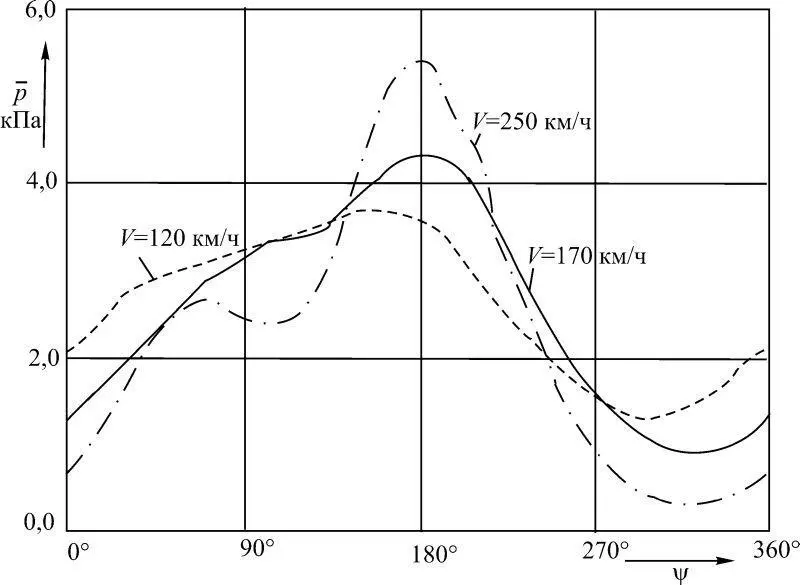
Рис. 5.1. Зависимость перепада давления на лопасти несущего винта вертолета Ми-8 от азимутального угла положения лопасти ( 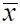= 0,41; 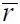= 0,4; Н = 1000 м; G = 11000 кг; n = 192 об/мин)

Величина пульсаций аэродинамической нагрузки в виде коэффициента перепада давления

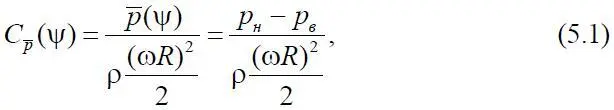
замеряемого в некотором сечении 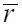= r / R лопасти НВ на расстоянии 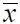= x / b от ее передней кромки, где R – радиус НВ, а b – хорда лопасти в сечении 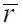, может быть оценена с помощью дисперсии

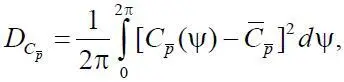
где Р н – давление на низшей стороне лопасти в точке 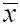сечения ;

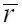Р в – давление на верхней стороне лопасти в этой же точке;

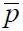– перепад давления в рассматриваемой точке;

ρ – плотность воздуха за бортом;

ω – частота вращения НВ;

ψ – азимутальный угол положения лопасти;

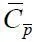– осредненное за один оборот НВ значение коэффициента перепада давления, определяемое как

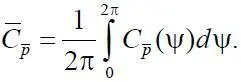
Исследования показали, что для идентификации продольной скорости движения НВ более удобно использовать информацию о величине среднего квадрата σ пульсаций коэффициента перепада давления, замеряемого в заданной точке хорды профиля,

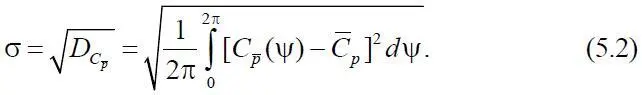
Величина среднего квадрата пульсаций коэффициента перепада давления теоретическим путем может быть определена следующим образом. В работе [2] представлен алгоритм вычисления коэффициентов тригонометрического полинома разложения аэродинамической нагрузки в виде коэффициента подъемной силы сечения лопасти:

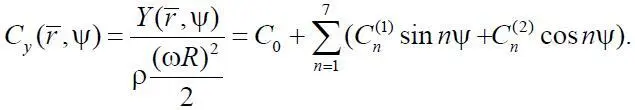
Используя связь между коэффициентом перепада давления , замеряемым в точке 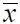сечения 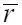, и коэффициентом 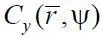подъемной силы этого сечения:

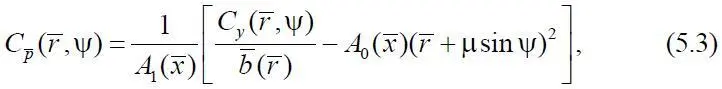
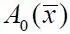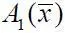где и – коэффициенты, зависящие для данной формы профиля лопасти только от положения точки 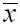съема перепада давления, а 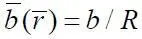– величина безразмерной хорды лопасти в сечении 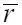, представим коэффициент перепада давления в виде тригонометрического полинома

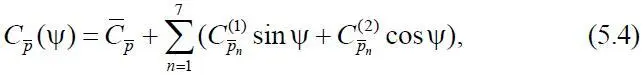
где

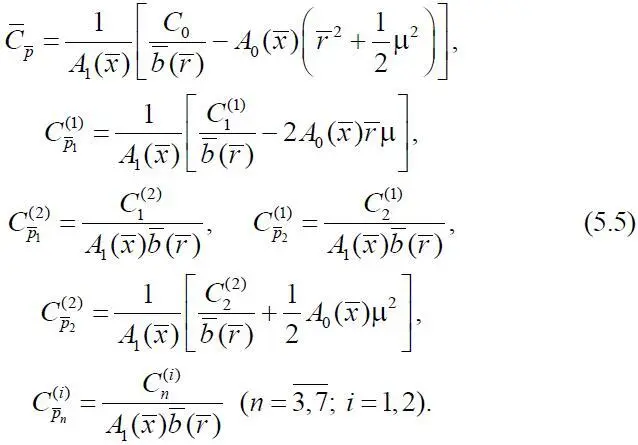
Подставляя (5.4) в (5.2), получим