Владимир Живетин - Введение в теорию риска (динамических систем)

где А – линейный оператор из Х в Y , λ – параметр.

Сегодня теория функциональных систем в математике включает в себя задачи о полноте, сложности выражения одних функций через другие, тождественных преобразованиях, анализ. С позиции прогнозирования и управления в эгосфере как функциональной системе нас интересуют функциональные уравнения процессов и полей:

на уровне макропередачи энергии;

на уровне микропередачи энергии, например от сердца и гипоталамуса к органам;

на уровне тонких энергетик – потенциалы: клеток, точек ноосферы, точек сердца и т. д.

Эгосфера включает в себя ряд подмножеств, обладающих различными свойствами, например дух, душа, аналитический ум, тело – на уровне эготопического пространства. Здесь необходимо применять для анализа, кроме пространства категорий, систему мер.

Решение любой количественной задачи [26] при моделировании, как правило, заключается в нахождении функции z , характеризующей состояние контролируемого объекта А эгосферы по заданным или измеренным значениям процесса и объекта В , связанного с А следующим уравнением:

z = R ( u ). (1.5)

В прикладных задачах u и z являются элементами метрических пространств U и Z соответственно, с расстояниями между элементами ρ u ( u 1, u 2), ρ z ( z 1, z 2), где u 1, u 2 U; z 1, z 2 Z. Метрика, как правило, определяется постановкой задачи. При этом метрические пространства Z и U выбираются необходимым образом так, чтобы:

– оценить близость элементов как средство описания окрестностей в пространствах Z и U ;

– обеспечить устойчивость решения для (1.5).

Возможна постановка этих задач для топологических пространств Z и U.

В качестве примера рассмотрим пространства эгосферы, включающие:

– геометрические объекты эгосферы – эготопическое;

– эгоэнергетическое (функциональное) – потенциальное пространство (микрообъекты);

– энергетическо-информационных процессов (тонких энергетик).

Представим взаимосвязь эготопического и эготопологического пространств (см. таблицу 1.1) [26].

Множество Ω* вещественных пространственно-упорядоченных объектов и систем включает клетки, органы, системы. Каждый элемент V i при переходе из эготопического в эготопологическое пространство преобразуется в элемент ω с помощью числовых функций, функциональных уравнений, т. е. V i ↔ ω.

Множество Ω* преобразуется в Ω с помощью операторов, в том числе с распределенными параметрами. При этом процедура построения Ω* включает в себя формирование теоретико-множественных объектов, а множество Ω содержит абстрактные объекты и операции (процессы), заданные различными математическими моделями.

Таблица 1.1

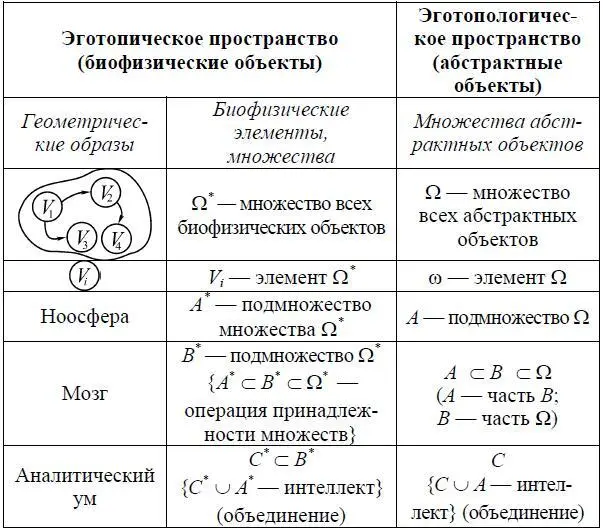
Выделим необходимые множества для дальнейших рассуждений.

Пусть дано множество Х , состоящее из элементов произвольной природы, называемых точками данного пространства, с введенной в этом множестве топологической структурой. Самый простой способ определения эготопологии G в данном множестве Х (эгосферы) заключается в непосредственном указании тех подмножеств множества Х , которые составляют топологию эгосферы. В зависимости от характера решаемой задачи, целей исследований может быть принята различная степень детализации (разделения).

Так, на макроуровне возможно выделение четырех подмножеств (согласно четырем подсистемам, формирующим структуру эгосферы как динамической системы). Таким образом, определим не все множества Х , создающие эготопологическое пространство, а только некоторые множества этих элементов, т. е. базу данной топологии, достаточные для того, чтобы все остальные элементы топологии получались как объединение множеств, которые составляют базу.

Всякое подмножество Х 0множества всех точек X данного топологического пространства Х превращается в топологическое пространство с топологией, элементы которой суть всевозможные множества вида X 0∩ Г, где Г – любой элемент топологии G. Так как эготопология есть множество некоторых подмножеств множества Х , то между различными топологиями в одном и том же множестве Х (эгосферы) устанавливается отношение порядка (по включению). При этом топология G 2больше (или равна) топологии G 1, если G 1есть подмножество множества G 2, а каждое открытое множество в G 1будет открытым и в G 2. Из понятия топологии выводятся и все остальные топологические понятия: замкнутое множество, окрестность точки, точка прикосновения, замыкание, операции замыкания.

Непрерывное отображение одного пространства в другое необходимо для введения связи в различной форме между подмножествами эгосферы и основными четырьмя (подсистемами эгосферы как динамической системы) соответствующими топологиями. Эгосфера как топологическое пространство включает в себя несколько непрерывных отображений элементов одного пространства в другое. При этом справедливо следующее: отображение f: X → Y (отображение топологического пространства Х в топологическое пространство Y ) непрерывно в точке х Х , если для любой окрестности О у точки y = f ( x ) Y в пространстве Y существует такая окрестность О х точки х в Х что f ( O x ) 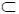O (условие Коши).

Если отображение f: X → Y непрерывно в каждой точке x X , то оно называется непрерывным отображением пространства Х в пространство Y.

Для непрерывности отображения f: X → Y каждое из следующих условий необходимо и достаточно:

– если х есть точка прикосновения какого-либо множества М 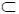Х , то f ( x ) есть точка прикосновения множества f ( М ) в Y ;

– полный прообраз f – 1(Г) всякого открытого в Y множества Г есть открытое множество в Х.

В эгосфере мы рассматриваем энергетическо-информационные пространства, составленные как из геометрических образов, так и в виде пространства функций, осуществляющих отображения энергетического потенциала из одного множества (пространства) в другое. В дальнейшем мы ограничимся одним метрическим пространством. В этом метрическом пространстве имеет место отображение информации из одного множества (пространства) в другое (для интеллектуального потенциала). На уровне тонких энергий, представляющих, как правило, случайные процессы, возможно применение теории потенциала. Потенциалы и метод потенциалов используются для решения задач электростатики и магнетизма. При этом рассматриваются притяжения масс произвольного знака или заряда.