Владимир Живетин - Введение в теорию риска (динамических систем)

2. Построение области допустимых значений параметра z , т. е. z доп , и оценка отклонения фактического значения z , т. е. z ф от z доп .

3. Обнаружение отказа соответствующего органа – контроль генетических и интеллектуальных энергетик и соответствующих программ.

4. Оценка функциональных возможностей эгосферы в среде жизнедеятельности, в том числе генетических и функциональных.

5. Позиционное наблюдение.

Средства программирования контролируемых и управляемых процессов:

– с помощью временных рядов;

– с помощью математических моделей энергетических, информационных и энергетическо-информационных процессов;

– при использовании оптимальных оценок;

– при помощи минимаксных оценок.

В эгосфере мы реализуем два вида управления: в интеллектуальном пространстве – U и – и в генетическом пространстве энергетик – U 2. При этом мы реализуем различные формы управления. Так, например, когда биофизическая энергетика покидает область допустимых состояний, т. е. x 2 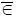Ω доп , мы проводим следующую операцию: вводим управление U 2в виде удаления больного органа в момент времени t 0и ожидаем в момент времени t 1событие x 2 Ω доп .

Выделим разновидности управлений , реализуемых в эгосфере:

– дискретное компенсационное;

– компенсационное непрерывное для внешних и внутренних возмущающих факторов;

– обеспечение функциональной независимости органов, в том числе в случае отказа органа;

– позиционное управление процессами;

– управление с использованием алгоритмов обучения информационно-энергетических полей и процессов.

В случае позиционного управления мы имеем ситуацию, изображенную на рис. 1.19. Здесь изображено: Ω доп – область допустимых состояний контролируемых энергетик; Ω кр – область критических состояний. При t = t 0исходное состояние было критическим, произведена операция, т. е. введено управление U ( t 0) так, чтобы достичь область Ω доп при t = t 1.

Рис. 1.19

Управление на интеллектуальном уровне (рис. 1.20).

1. Задача построения u и ( t ) для тех, кто сам не может этого сделать, – нужна программа управления, помощь в анализе.

Рис. 1.20

2. Задача построения u и ( t ) для тех, кто сам не может построить цель и способ, соответствующие своим возможностям, – помощь в синтезе.

3. Промежуточная задача построения u и ( t ) для тех, кто с ошибками формирует цель и способ ее достижения.

Можно искать решение в условиях неопределенности, либо можно искать решение в пространстве случайных функций, например с помощью теории потенциала или применяя методы теории катастроф. Во всех случаях мы хотим обеспечить пребывание энергетического потенциала E ч ( t ) в области Ω доп .

Указанные выше свойства объектов эготопологического пространства можно распространить на динамические системы, в совокупности своей формирующие иерархию интеллектуально-энергетических динамических систем (рис. 1.13).

Анализ характеристик риска будем осуществлять на двух уровнях: качественном и количественном. Качественный анализ может быть сравнительно простым, его главная задача – определить совокупность факторов, влияющих на риск и безопасность на различных уровнях динамической системы. Количественный анализ риска сводится к численному расчету размеров риска отдельных подсистем, отдельных индикаторов состояния системы и риска и безопасности системы в целом. Качественный анализ предшествует количественному, он осуществляется на уровне структур и учитывает функциональные особенности и свойства подсистем, наполняющих динамическую систему.

Согласно существующим теоретическим основам, количественный расчет значений риска и безопасности динамической системы может быть осуществлен при помощи:

– использования аналогов;

– экспертных оценок;

– динамического моделирования;

– статистических испытаний;

– вероятностных методов.

Наиболее распространенным методом оценок риска в настоящее время является метод статистических испытаний. Однако этот метод работает только для функционирующих систем.

Недостатки метода статистических испытаний:

– необходим большой объем исходных данных в течение длительного времени функционирования реально существующей динамической системы, когда полученные материалы часто теряют свою актуальность и значимость;

– их невозможно получить, например, на этапе создания системы и обеспечения их реализации;

– практически невозможно оценить влияние отдельных подсистем и факторов на показатели риска.

Этих недостатков лишен вероятностный метод, основанный на математических моделях процессов и полей, создаваемых динамической системой в процессе функционирования [44].

Выделим следующие уровни анализа риска и безопасности.

Первый уровень – осуществляется анализ, прогнозирование и управление конечной целью (как сейчас и не только в экономике).

Второй уровень – все подсистемы в совокупности подвергают анализу на предмет риска и безопасности.

Третий уровень – каждая подсистема анализируется как система со структурой, а затем анализ риска и безопасности производится в совокупности для своей системы.

При синтезе и анализе математических моделей процессов и полей динамической системы необходимо учитывать следующие особенности:

– в процессе функционирования динамической системы всегда решается множество задач, некоторые из них, в силу объективных причин, оказываются противоречащими главной цели;

– функциональные свойства подсистем и системы в целом изменяются под влиянием внутренних и внешних факторов риска;

– в процессе функционирования в подсистемах происходят процессы старения, деградации.

В процессе функционирования динамическая система получает на вход из окружающей среды потоки ресурсов R вх = R вх ( E вх , J вх , m вх ) в виде энергетических E вх , информационных J вх , массовых m вх компонент. Система перерабатывает R вх и отдает в среду потоки X ( t ), в том числе потоки ресурсов R вых = R вых ( E вых , J вых , m вых ) для динамических систем внешней среды.