Владимир Живетин - Введение в теорию риска (динамических систем)
- Название:Введение в теорию риска (динамических систем)
- Автор:
- Жанр:
- Издательство:Изд-во Института проблем риска, Информационно-издательский центр «Бон Анца»
- Год:2009
- Город:Москва
- ISBN:978-5-98664-052-5, 978-5-903140-63-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Живетин - Введение в теорию риска (динамических систем) краткое содержание
В работе вводятся первичные и вторичные показатель риска как для классических информационно-энергетических систем, так и для суперклассических – интеллектуально-энергетических систем.
Первичные показатели риска характеризуются множеством безопасных состояний, рассчитанных согласно, например, теории устойчивости; вторичные показатели риска представляют собой вероятности выхода динамической системы в область критических состояний с учетом свойств систем контроля и управления.
Полученные результаты позволяют осуществить математическое моделирование прогнозирования и управления рисками различных динамических систем, включая интеллектуально-энергетические.
Введение в теорию риска (динамических систем) - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
В качестве внешних возмущающих факторов W будем выделять следующие события и процессы:
– созданные средой (так, например, биосферой), на которые человек не может влиять, которыми он не может управлять; это, как правило, чрезвычайно редкие события и процессы, так, например, стихийные бедствия, которые невозможно прогнозировать достоверно;
– созданные в результате деятельности человека в окружающей среде, имеющие определенную повторяемость и достаточно четкое описание их возникновения в виде модели;
– как итог, обусловленный управляющими воздействиями, например, со стороны социально-экономических систем.
Основные потери (риски) динамической системы формируются в подсистемах целеполагания (подсистема 1) и целедостижения (подсистема 2). Целеполагание, как правило, осуществляется на качественном уровне и позволяет судить лишь об общем направлении работ в виде генеральной цели. В подсистеме (2) генеральная цель разбивается на совокупность более частных, более простых и конкретных подцелей, т. е. проводят квантификацию целей.
Осуществив квантификацию, получаем многоуровневое иерархическое дерево целей. Для обеспечения полноты в набор целей нижнего уровня включаются цели, характеризующие различные стороны процесса функционирования системы. Дерево целей позволяет иметь полный перечень задач анализа потерь для подсистем любого уровня.
Процесс квантификации цели завершен, когда получен набор количественно измеримых подцелей, связанных с показателями функционирования динамических подсистем.
Каждый из таких показателей характеризует состояние ( E, J, m ) отдельных подсистем каждого уровня и системы в целом.
В процессе реализации цели в каждой из подсистем динамической системы (рис. 1.8) создаются потери, которым соответствуют нижеследующие функциональные риски.
1. Происходящие при реализации цели вследствие того, что результат воздействия (реализующего решения) с погрешностями δ U 3управления подсистемой (3) структуры, как в данный момент, так и в последующие вызовут отклонение динамической системы от расчетного или наилучшего значения цели с последующим выходом в Ω кр .
Вероятностную меру этой потери характеризует величина риска R 3, которую назовем риском действия.
2. Обусловленные несовершенством методов и средств, а также ресурсов, с помощью которых формируются погрешности δ U 2при формировании управления U 2, обусловливающие выход динамической системы в область Ω кр .
Вероятную меру R 2такой потери назовем риском управления.
3. Обусловленные ошибками δ U 1процесса целеполагания, в том числе ошибками идентификации структурно-функциональных свойств динамической системы и ошибками контроля, обусловливающими выход динамической системы в Ω кр .
Вероятностную меру R 1такой потери назовем риском целеполагания.
4. Происходящие при реализации цели вследствие того, что оценка цели, например, при ее измерении и построении Ω доп включает погрешности δ U 4, которые обусловливают погрешности целеполагания, целедостижения (управления), приводя к выходу динамической системы в Ω, кр .
Вероятностную меру R 4такой потери назовем риском оценки.
При этом потери Δ Ц при целереализации можно представить в виде: Δ Ц = Δ Ц (δ U 1, δ U 2, δ U 3, δ U 4, X, Y, t ) где: δ U 1 – погрешности целеполагания; δ U 2 – погрешности управления (целедостижения); δ U 3 – погрешности действия (целереализации); δ U 4 – погрешности оценки (контроля).
Отметим основную проблему: идентификация в процессе формирования цели подсистемой (1) целеполагания должна быть такой, чтобы потоки ресурсов на выходе динамической системы R вых = R вых ( Е вых , J вых , m вых ) достигали максимально допустимое значение.
Можно говорить о первом приближении опасного и безопасного состояний системы, когда оцениваются ее выходные координаты в текущий момент времени. Так, например, на стол главы правительства поступает информация, что валовый национальный продукт за прошлый год в норме. Но в этот год подсистема (2) и ее потенциал покинул Ω доп [25, 34], однако он не оценивается. Здесь критическая ситуация, однако динамическая система не «осознает» ее, так как не контролирует и не управляет.
1.4.2. Риск управления. Факторы риска
Проблема управления рисками и обеспечения безопасности динамической системы состоит в оценке (измерении) ее состояния и в создании такого управления, которое обеспечит условие ( X, Z )  Ω доп и исключит ситуацию ( X, Z )
Ω доп и исключит ситуацию ( X, Z )  Ω кр (рис. 1.21), где Z = ( z 1, z 2, z 3, z 4); z i – процессы, формируемые соответствующими подсистемами.
Ω кр (рис. 1.21), где Z = ( z 1, z 2, z 3, z 4); z i – процессы, формируемые соответствующими подсистемами.
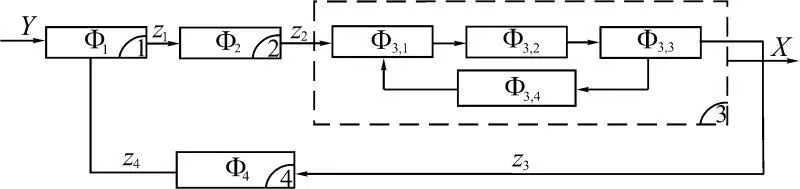
Рис. 1.21
Ограничиваясь индикатором x ( t ) = X ( t ), для реализации указанной цели выделим два управления ( u 1, u 2):
u 1 – осуществляет ограничение величины отклонения фактического значения х (обозначим его х ф ) от расчетного (заданного) или номинального х н ;
u 2 – осуществляет предотвращение выхода х ф в Ω кр , т. е. предотвращает событие x ф  Ω к .
Ω к .
Первое управление включает два управления:
u 1,1 – реализующее номинальные значения х , т. е. х н ;
u 1,2 – осуществляющее стабилизацию или нейтрализацию отклонений процесса х ф от х н .
Процесс х ф , в силу зависимости от случайных внешних W ( t ) и внутренних V ( t ) факторов риска, также относится к случайным процессам. При этом х ф = m x + Δ x , где m x = m x ( t ) – математическое ожидание х ф , в общем случае функция времени, часто совпадающая с х н ( t ); Δ x = Δ x ( t ) – отклонение х ф от математического ожидания, в общем случае случайный процесс.
Задача управления u 1, 2состоит в компенсации Δ x таким образом, чтобы Δ x было минимальным. Отметим, что в общем случае имеет место Δ x = Δ 1 х + Δ 2 х , где Δ 1 x обусловлен внутренними возмущающими факторами, т. е. Δ 1 x = Δ 1 х ( V ); Δ 2 x – внешними, т. е. Δ 2 x = Δ 2 х ( W ).
Как правило, в системах, формирующих управления u 1,2и u 1,1, не предусмотрено обеспечение условия x ф  Ω доп . Последнее условие обеспечивает управление u 2. В случае отсутствия u 2возникает событие x ф
Ω доп . Последнее условие обеспечивает управление u 2. В случае отсутствия u 2возникает событие x ф 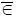 Ω доп .
Ω доп .
Интервал:
Закладка:










