Владимир Живетин - Введение в теорию риска (динамических систем)

– область критических состояний Ω кр ( х ), когда динамическая система не способна достичь поставленную цель в силу того, что, например, < 0, но способна возвратиться в Ω доп ;

– область безвозвратных состояний или энергетической смерти, когда θ = 0, включая энергию, получаемую от среды.

Приведем классификацию областей состояния динамической системы.

Уровень 1. Одна координата х динамической системы подлежит ограничению, при этом имеет место одностороннее ограничение по минимуму или по максимуму. Динамическая система находится в квазистационарном режиме.

Уровень 2. Один параметр х динамической системы подлежит двустороннему ограничению: по минимуму и по максимуму. Динамическая система находится в квазистационарном режиме функционирования.

Уровень 3. Многопараметрическое одностороннее ограничение векторного параметра х = ( х 1, …, х n ); многопараметрическое двустороннее ограничение. Динамическая система находится в квазистационарном режиме.

Уровень 4. Нестационарный режим функционирования, когда скорость изменения параметров 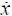≠ 0.

Уровень 5. Хаотический процесс изменения х ( t ).

Проблема построения области допустимых состояний решалась, решается и будет решаться широко и глубоко в силу ее большой значимости для среды жизнедеятельности. Пока здесь имеет место некоторая незавершенность для физических систем, где приложен талант многих великих ученых.

Часто мы познаем границы Ω доп так же, как животные: через потери (так, например, флаттер крыла самолета, колебания шимми колеса самолета [31]). Область допустимых состояний Ω доп имеет границу S доп , например, точку x доп в одномерном случае для стационарного процесса, для случая двустороннего ограничения в виде изолированных точек х н доп, х в доп – нижнего и верхнего значений соответственно. Область критических состояний имеет границу S кр , которая отстоит в одномерном случае на некоторую величину запаса Δ от S доп .

В общем случае, когда х доп = х доп ( t ), для различных динамических систем на границе S кр формируются процессы:

– детерминированные;

– квазидетерминированные;

– стохастические;

– квазистохастические.

Можно выделить две крайности для границы S кр : жесткая и «эластичная». В первом случае нарушение границы S кр приводит к «смерти» динамической системы, когда невозможен возврат в Ω доп , во втором случае – к такой потере функциональных возможностей, когда возможен возврат в Ω доп . Для построения математической модели оценки риска необходимо иметь достоверную информацию как о самих Ω доп , S доп , Ω кр , S кр , так и об особенностях функционирования динамических систем при их достижении.

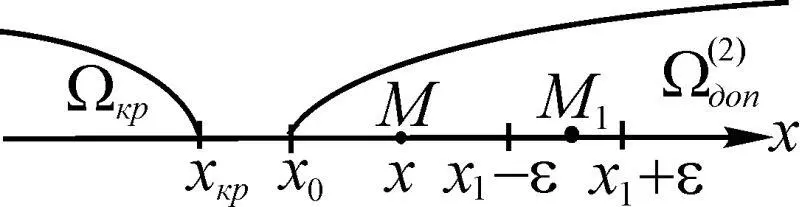
Рис. 1.23

Приведем в качестве примера области состояния такой динамической системы, как человек (рис. 1.23). Пусть в точке М 1= М 1( х 1), и ее окрестности ( x 1± ε) в момент t энергия Е обеспечивает комфортное его состояние. За время жизни фактическое состояние организма, характеризуемое точкой М 2= М ( х ), перемещается в сторону х 0критической области. Чем дальше от х 1, т. е. ближе к х 0, при увеличении ρ( M, M 1) состояние человека ухудшается, достигая границы S доп ( х = х 0). За границей S доп начинается область динамического хаоса, когда Е ≠ 0, но близко к нему. Катастрофа происходит тогда, когда Е = 0, организм полностью отключается при достижении критической точки х кр .

Области допустимых значений параметров контроля и управления (состояний) для динамической системы, как правило, определяются в статических условиях. В основном это обусловлено простотой реализации систем контроля и управления. При переходе к динамической области состояния возникает многофакторное ее описание, и реализация систем контроля становится затруднительной.

Существуют два пути учета динамики:

1) уменьшение области Ω с доп , выбранной в статике;

2) учет допустимости выброса, т. е. введение в расчет допустимой величины времени выброса τ доп , в область критических состояний.

При этом область допустимых состояний Ω доп включает в себя области с фиксированными границами: устойчивости, наблюдаемости, управляемости, идентифицируемости. Сегодня эти области Ω( C ) для динамических систем технического содержания получены в виде параметрических ( C ) соотношений. Однако при заданных С эта область зависит от ( E, J, m ), которые изменяются практически во всех системах, в том числе технических и биосистемах. Другое дело – причины, обусловливающие изменение θ = ( E, J, m ), различные для различных систем.

Отметим, что в области допустимых состояний динамической системы реализуются регулярные динамические процессы, когда процесс достижения поставленной цели контролируем и управляем. В области критических состояний динамических систем реализуются хаотические динамические процессы – непрогнозируемые, когда поставленная цель не достигается.

Объекты, которые можно различать и идентифицировать, должны находиться в режиме регулярной динамики. В режиме хаотической динамики динамическая система не идентифицируется. Процесс пребывания в критической области происходит различным образом как для различных динамических систем, так и для различных параметров одной и той же динамической системы. Так, например, для самолета такое критическое состояние, как сваливание в штопор и движение в нем на большой и малой высоте, завершается по-разному. В первом случае самолет, как правило, возвращается в область допустимых состояний, во втором – происходит пересечение с поверхностью земли, т. е. наступает энергетическая «смерть». При этом возникает проблема допустимости и недопустимости пребывания динамической системы в области критических состояний, так, например, хаотический режим свойственен не только динамическим системам, но и социальным и в частности их «атому» – человеку. Во всех случаях источником такого режима является функциональная особенность динамической системы, возникающая под действием внутренних и внешних факторов риска. Так, клинической смерти человека предшествуют хаотические режимы работы сердца. Если такие режимы ограничены по времени, то возможен выход из Ω кр в Ω доп .