Владимир Живетин - Введение в теорию риска (динамических систем)

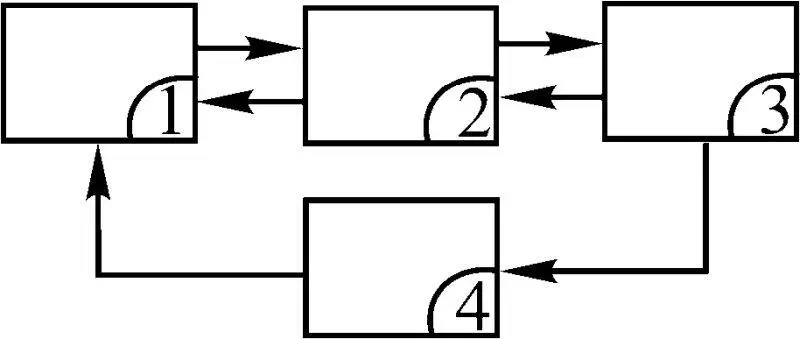
Рис. 1.26

Рассмотрим, в каком виде, какая информация нужна каждой подсистеме структуры, чтобы подсистемы могли реализовывать необходимые алгоритмы обработки статистических данных.

Сначала перечислим функциональные свойства подсистем .

Подсистема 1 порождает структуру системы в целом, способную идентифицировать процессы достижения цели (целеполагание), т. е. реализует синтез.

Подсистема 2 выполняет параметрический анализ, отражающие точностные характеристики.

Подсистема 3 реализует смешанные алгоритмы, синтез и анализ.

Подсистема 4 проводит оценивание законов, функций и плотностей вероятностей.

Процесс оценивания в подсистеме 4 непосредственно связан с величиной показателей достоверности знаний, основанных на:

– синтезе и идентификации;

– теории анализа внутренних компонент;

– формировании прикладных методов;

– оценке результатов.

Отметим, что идентификация структуры динамических систем возможна с использованием структуры выходных процессов динамической системы, так, например, с помощью моментных характеристик.

В подсистеме 1 (рис. 1.26) формируется показатель качества алгоритма, устанавливающего связь между функциональными свойствами подсистем структуры и выходным процессом системы. При этом показатель качества есть некоторая характеристика, определяющая соответствие алгоритма его назначению, оценивающая пригодность алгоритма для решения поставленной задачи и достижения искомой цели. Так, для оценки вероятностной характеристики в данный момент времени достаточно FN- диаграммы, а для прогнозирования той же характеристики необходима как минимум корреляционная функция процесса. При этом показатель качества, как правило, отражает одну из сторон функционирования и область применения алгоритма.

В основу построения математической модели, порождающей стохастические процессы, положим вероятностное пространство, сформированное согласно аксиоматическому методу – системе аксиом Колмогорова. Воспользуемся вероятностной моделью испытаний на базе системы аксиом со структурой [44].

При этом вероятностное пространство характеризуется набором математических объектов (Ω, , P ), где Ω – пространство исходов или пространство элементарных событий, множества А из – события, а P ( A ) – вероятность события А.

Базовой основой аксиоматической теории вероятностей служат теория множеств и теория меры. Структура построенных нами вероятностных пространств должна исчерпывать структуру процессов и полей, порожденных динамической системой, для исследования которых создано пространство. Наиболее трудный этап – установление связи между структурой процессов и структурой моделей самой динамической системы, сформировавшими эти процессы.

При построении стохастических математических моделей для математического описания физических объектов используются два принципа [44]:

– аксиоматический А.Н. Колмогорова A* 1, априори вводимых моделей;

– статистический фон Мизеса A* 2, апостериори вводимых моделей.

Подход A* 1имеет в основе макромир, идет от него к микромиру методом дедукции; подход A* 2имеет в основе микромир, идет от него к макромиру (методом индукции).

Эти подходы могут соединиться через структуру макромира, содержащую подсистемы микромира. Объединить эти два подхода может единая структура математической модели динамических систем. При этом A* 1идет сверху вниз, а A* 2 – снизу вверх при изучении одной и той же динамической системы. Часто их пути расходятся: изучая одну и ту же динамическую систему, они приходят к различным конечным структурам моделей динамических систем.

Согласно сказанному, рассмотрим вероятностную модель, вероятностное пространство эксперимента с конечным пространством исходов. В результате изучения подхода, созданного Колмогоровым, получена система и осуществлен структурно-функциональный синтез вероятностной модели Колмогорова, представленный на рис. 1.27.

Рис. 1.27

На рис. 1.27 обозначено: ω – исходы динамической системы; Ω(ω) – множество исходов; М 0 – модель изучаемой динамической модели (фактическая модель); M * 0 – модель М на множестве исходов; M* 1 – модель М на алгебре подмножеств; M 1 – модель, созданная в результате синтеза и анализа множества Ω(ω), в результате чего мы ввели меру Р или в общем случае (Ω, А, Р ), т. е. создали искомую модель М 1.

С целью анализа статистического подхода, созданного фон Мизесом, на рис. 1.28 схематично представлена взаимосвязь и различие на структурно-функциональном уровне рассматриваемых принципов построения математических моделей. Здесь случайные внешние факторы обозначены как W, W 1, W 2.

Рис. 1.28

Исходная ситуация в подходе Колмогорова обусловлена наличием структуры Σ, а функциональные свойства Ф ст получены по материалам статистических испытаний. Исходная ситуация в подходе фон Мизеса обусловлена отсутствием структуры Σ, а функциональные свойства Φ получены по материалам статистических испытаний (Σ ст , Ф ст ).

В качестве меры отличия моделей M 0, M 1, M 2принимается отличие свойств созданных ими множеств, так, например, дисперсии погрешностей, обусловленных величинами Δ 1= | x 0– x 1| и Δ 2= | x 0– x 2|, где x 0, x 1, x 2 – случайные величины, порожденные соответственно моделями M 0, M 1, M 2.

В общем случае в процессе функционирования динамических систем измерению и ограничению подлежат многомерные процессы. В дальнейшем ограничимся рассмотрением одномерного и двумерного процессов. В этом разделе мы рассмотрим несколько моделей процессов контроля индикаторов х ( t ) состояния как динамической системы, имеющих односторонние и двусторонние ограничения. При одностороннем ограничении возможны следующие ситуации.

1. Простейшая ситуация.

Ограничиваемый процесс х ( t ) – одномерный, ограничения односторонние, в нашем примере – по минимуму (рис. 1.29), значение х 1 доп вычислено в системе контроля точно, без ошибок, ошибки измерения δ х = х ф – х изм равны нулю, т. е. х изм = х ф ; динамикой процесса х ( t ) и ошибками управлений можно пренебречь. При этих условиях критическое значение х , т. е. х кр , совпадает с х 1 доп . Такую ситуацию и модель (систему) будем считать идеальной.