Владимир Живетин - Введение в теорию риска (динамических систем)

Состояние динамической системы со структурой характеризуется различной степенью упорядоченности (рис. 1.24) с односторонним ограничением по минимуму, свойственной областям состояний Ω 1, Ω 2, Ω 3, на которые разделяется критическая область состояний Ω кр динамической системы. В области Ω 1возможна частичная потеря функциональных свойств, когда возможно самовосстановление. В области Ω 2требуются специальные меры восстановления функциональных свойств динамической системы, динамика функциональных свойств которых хаотическая. Только после принятия специальных мер динамическая система способна выполнять исходную цель, возвратившись в область допустимых состояний. В области Ω 3находятся те динамические системы, которые не подлежат восстановлению и сами являются источником хаоса для других динамических систем.

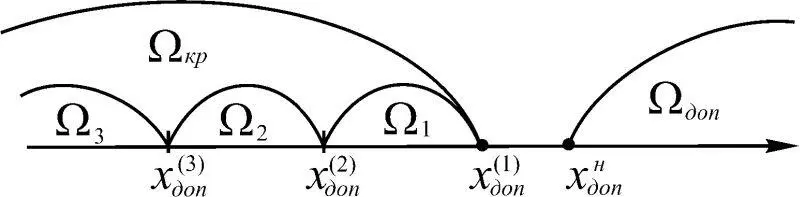
Рис. 1.24

Принцип минимальных потерь (риска) свойственен всем динамическим объектам бытия, и его реализация со стороны человека является основополагающей. Однако здесь не все благополучно и, на наш взгляд, делаются начальные вклады в этот процесс. Это обусловлено сложными связями динамических систем мегамира, которые включают в себя динамические системы макромира, а последние включают в себя динамические системы микромира, включающие в себя в свою очередь объекты тонкого мира. При этом одна и та же динамическая система рассматривается нами в зависимости от уровня проникновения в ее сущность:

– детерминированная, а процессы, порожденные ею, мы относим к регулярным;

– квазидетерминированная, а процессы, порожденные ею, мы относим к квазидетерминированным, включающим стохастическую компоненту как вспомогательную (неосновную);

– стохастическая, а процессы, порожденные такой динамической системой, мы относим к случайным.

Так, например, для динамической системы, описываемой математической моделью вида = f ( x, W, V, t ), где x, W, V – выходная координата, внешние и внутренние возмущающие факторы риска соответственно, на различных этапах анализа риска рассматривают следующие модели: 1) 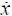= f ( x, t ), 2) 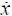= f ( x, V, t ), 3) = f ( x, W, t ). Если W в последней модели является квазидетерминированным процессом, то принимаем x ( t ) квазидетерминированным, если во второй модели V – стохастический, то процесс x ( t ) также стохастический.

В каждом из миров: макро-, микро– и тонком мире – имеют место различные цели функционирования динамической системы, различные функциональные возможности их подсистем с соответствующими потерями и рисками. В зависимости от того, из какого пространства происходит оценка, вводится соответствующая мера. Если из макромира оценивается система микромира, то имеют место стохастические процессы; если наоборот – то имеют место детерминированные.

Мы часто рискуем, не подозревая об этом. Так было, например, с флаттером. При этом наш риск связан с незнанием законов явлений. Здесь работают детерминированные показатели, а выход в Ω кр , когда возникает флаттер, обусловливает разрушение крыла самолета, когда наступает энергетическая «смерть» динамической системы [30, 31].

При анализе риска мы оцениваем, прогнозируем и управляем вероятностным процессом, а в качестве меры риска принимаем вероятности. Такой подход связан с особенностями принятых моделей, он имеет место для любой системы из иерархии систем. Так, например, для человека это:

– макроуровень на уровне тела и соответствующие риски;

– микроуровень на уровне органов и соответствующие риски;

– системы, реализующие алгоритмы контроля и управления, т. е. тонкий мир и соответствующие риски.

На каждом из этих уровней (миров) мы обнаруживаем допустимые и критические значения энергий и энергетическо-информационных потенциалов. При этом для анализа рисков необходимы:

– модель биофизическая в эготопическом пространстве;

– модель теоретическая в эготопологическом пространстве;

– процедуры теоретического расчета Ω доп , Ω кр ;

– процедуры построения вероятностей риска P ;

– модель систем контроля, прогнозирования и управления эгосферными рисками.

При формировании показателей риска и безопасности динамической системы возникает ряд проблем в связи с тем, что система обладает структурой, каждая из подсистем которой имеет возможность независимого изменения своего потенциала. Так, показатели риска и безопасности динамических систем, созданных человеком, формируются на следующих этапах их жизненного цикла [17, 21]:

– научно-исследовательском;

– проектно-конструкторском;

– производственном;

– эксплуатационном.

Существенным фактором выступает временной интервал оценки риска и безопасности для различных объектов. Так, например, экономика страны оценивается, как правило, за год работы, отрасли – за квартал, завода – ежемесячно, станка – ежедневно.

Таким образом, задача построения области включает в себя:

– обоснование совокупности параметров x состояния системы, подлежащих контролю и ограничению;

– разработку метода количественного расчета фактических значений параметров x с заданной степенью достоверности;

– задание и обоснование критических значений x , т. е. x кр , где x = ( x 1, …, x n );

– разработку методов оценки погрешностей измерения параметров x с расчетной степенью достоверности;

– разработку метода численного расчета x o доп .

В общем случае область допустимых измеренных посредством средств контроля значений Ω o доп за счет погрешностей измерения отличается от Ω доп , и, кроме того, Ω o доп зависит от x ф , т. е. фактических значений индикаторов. Например, для рыночной социально-экономической системы Ω o доп = Ω o доп (x, у, z ), где x = ( x 1, x 2, … ) – индикаторы производственной сферы; у = ( у 1, у 2, … ) – индикаторы финансовой сферы; z = ( z 1, z 2, z 3, z 4) – индикаторы социальной среды с соответствующими подсистемами.

Особенность разрабатываемой модели заключается в необходимости рассмотрения вероятностных процессов, порождаемых динамическими системами, обладающими структурно-функциональными свойствами. Такие системы обладают интеллектуально-энергетическим потенциалом, для контроля которого используется информационно-измерительная система.