Владимир Живетин - Введение в теорию риска (динамических систем)

Риск управления обусловлен следующими факторами риска:

– в подсистеме (2), осуществляющей управление;

– погрешностями программ целеполагания, целедостижения;

– недостатком ресурсов систем управления для компенсации W и V.

Для функционирующей динамической системы модель структурно-функционального состояния имеет вид:

F (Σ, Ф, E, J, m ) = 0,

где E, J, m – энергия, информация, масса соответственно, Σ, Φ – структура и функциональные свойства подсистем и системы в целом; F – нелинейный интегродифференциальный оператор.

Если θ = ( E, J, m ) находится в области допустимых состояний, то имеет место функционирующая динамическая система. Если θ = ( E, J, m ) покинула область Ω доп , но не приняла нулевые значения, то для системы наступает хаотический режим, когда она не способна выполнять исходное целевое назначение, например создавать свободные энергии для компенсации W, V и осуществления своей эволюции.

В общем случае динамическая система с иерархической структурой описывается математической моделью вида

F (Φ 1, Φ 2, Φ 3, Φ 4, θ, X, Y ) = 0,

где F ( · ) – нелинейный интегродифференциальный оператор; Φ 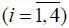– функциональные свойства соответствующих подсистем (их модели); Y – входные факторы; X – выходные факторы, подлежащие контролю и ограничению.

В свою очередь модель каждой подсистемы имеет вид:

F i ( Φ i ,1, Φ i, 2, Φ i, 3, Φ i, 4, θ i , x i , y i ) = 0 .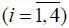

В качестве примера на рис. 1.21 приведена структура динамической системы, в которой Ф 3представлена в свою очередь в виде структуры, содержащей подсистемы Ф 3,1, Ф 3,2, Ф 3,3, Ф 3,4. Такая структура имеет место, например, для социально-экономической системы, когда подсистема (3) представляет экономическую систему, а на более низком уровне находится человек.

В качестве примера рассмотрим следующие крайние ситуации.

I. Если мы хотим оценить критическую ситуацию риска и безопасности динамической системы в данный момент времени, то z i Ω кр подсистемы можно рассматривать как независимые события.

II. Если же мы хотим анализировать возможность управления рисками и безопасностью на некотором интервале времени, то мы должны прогнозировать процессы. В этом случае z 1, z 2, z 3, z 4будут зависимыми процессами, а z i Ω ( i ) кр – зависимыми событиями.

В случае I критическая ситуация возникает не только тогда, когда Ц Ω кр , но и тогда, когда z i Ω ( i ) кр 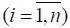, где Ц = Х.

Если в государственной системе власти z 1 Ω (1) кр , то имеет место постоянная цель Ц = const = Ц ( t 0), не корректируемая во времени. Это застой системы.

Аналогично, если z 2 Ω (2) кр , то имеют место застойные или ложные пути и методы достижения цели.

Если z 3 Ω (3) кр , то имеет место падение потенциала E 3.

Если z 4 Ω (4) кр , вся система деградирует, несмотря на то, что z i Ω доп .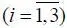

Пусть целью динамической системы является создание потенциала θ = ( E, J, m ), который формируется на выходе системы, т. е. X = θ. Для того чтобы система функционировала сама и выполняла задачи от иерархии, она должна создавать Х не менее X доп . При этом она должна получать из иерархии ресурсы Υ – то, что сама не может производить. Часть созданного потенциала θ = θ 1+ θ 2в виде θ 2она отдает в среду тем динамическим системам, которые не могут его производить.

Будем предполагать, что система на иерархическом уровне имеет обратную связь. Так, если θ 2 Ω (1) кр , то ресурсы, поступающие из внешней среды, на входе подсистемы (3) уменьшаются до величины у 3 Ω (2) кр , и θ 2уменьшается. Такова реальность, имеющая место в иерархии динамических систем. Критическая ситуация для динамической системы в целом зависит от критической ситуации каждой подсистемы, когда z i Ω ( i ) кр 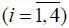. В итоге имеет место проблема: оценить риск иерархии динамических систем, самой динамической системы.

В дальнейшем мы ограничимся самой динамической системой. Полученные результаты могут быть обобщены на иерархию динамических систем. При этом в случае объединения двух или более динамических систем возникают особенности как при моделировании его состояния, так и при оценке суммарного риска [17, 24, 30, 31]. Факторы риска на структурно-функциональном уровне формируются в процессе отклонения объектов бытия от основных принципов, что обусловливает изменение функциональных свойств систем и приводит к их неспособности творить исходные цели. Это обусловливает отклонение их параметров состояния от нормы и выход в область критических состояний с последующей патологией (стандартным отклонением от норм). При этом нарушение законов передачи энергетическо-информационных полей с различных уровней иерархии динамических систем разрушает сначала функциональные свойства подсистем, их программы, что влечет за собой частичную или полную деструктуризацию, т. е. потерю одной из подсистем. В итоге динамическая система не в состоянии обеспечить реализацию поставленной цели, а после этого она либо отмирает, либо мутирует в новый объект, чуждый исходному.

В качестве примера рассмотрим процесс, характеризующий смерть одной из цивилизаций.

Один из сценариев смерти цивилизации (например, Римской империи) начинается с того момента времени, когда материальные ресурсы ( R м ) достигают максимальной величины (которую назовем критической ( R м ) кр ), а духовные ( R д ) резко падают до минимально допустимых ( R д ) кр . При этом имеем ( R д ) кр = f (( R м ) кр , t ) [28].

Модель подлежит разработке с целью прогнозирования момента времени достижения ( R м ) кр и ( R д ) кр . Прежде всего отметим, что источником формирования этносов, суперэтносов, империй, цивилизаций являются не материальные, а духовные ресурсы.