Владимир Живетин - Введение в теорию риска (динамических систем)

Для построения такой модели человечество накопило большое количество подобных процессов-сценариев: Египет, Индия, Китай, Древний Рим, Израиль, Россия [28]. Как показывает анализ структурно-функционального состояния этих цивилизаций, имеют место следующие подсистемы с их наполнением человеческими духовными ресурсами R д [28]:

– подсистема (1) целеполагания R (1) д 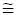5 %,

– подсистема (2) целедостижения R (2) д 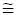5 %,

– подсистема (3) целереализации R (3) д 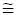70 %,

– подсистема (4) контроля целесостояния R (4) д 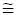5 %,

– шудра (потерянные ресурсы) R (5) д 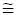15 %.

Ресурсы духовные R ( i ) д 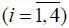по своему нравственно-интеллектуальному потенциалу не должны уменьшаясь выходить из области допустимых значений Ω ( i ) доп в область критических значений Ω ( i ) кр . В случае если это произошло, процессы целеполагания и целедостижения создают критическую ситуацию в подсистеме целереализации (3). Возникает противостояние целей, методов и средств ее достижения. В итоге наблюдается резкое падение энергетического потенциала, наступает энергетическая смерть.

Для предотвращения этого необходимо найти способ оценки уровней нравственно-интеллектуального потенциала в подсистемах, выявить уровень допустимых и критических значений, начиная с которых происходит деструктуризация системы. При этом подсистемы есть, но их функциональный потенциал ничтожно мал в силу свойств личностей, их наполняющих, как сейчас в России.

При создании такой модели следует учесть один из важных факторов подобных систем, а именно:

– единство разума , структурно-функциональных свойств различных людей планеты, которое становится очевидным, если рассмотреть их творения [21, с. 72];

– более тонкое творение человечества – единая структура культуры [21, с. 102].

Возникновение опасного состояния динамической системы может быть представлено как последовательность нижеследующих событий. При одностороннем ограничении по минимуму возможны следующие ситуации.

1. Появление события А , обусловленного отклонением х под влиянием W или/и V. В результате такого воздействия отдельные компоненты вектора х (или все в совокупности) покидают область Ω доп и попадают в Ω кр . Событие А обозначим А = { x Ω кр }. Вероятность события А обозначим Р ( А ) (рис. 1.22).

2. Пусть событие А происходит на интервале времени τ большем, чем τ 0, за которое в динамической системе завершаются все переходные процессы, и тогда она не может возвратиться в Ω доп . Таким образом, опасное состояние динамической системы наступает тогда, когда реализуются два события ( А, В ), где В : (τ > τ 0).

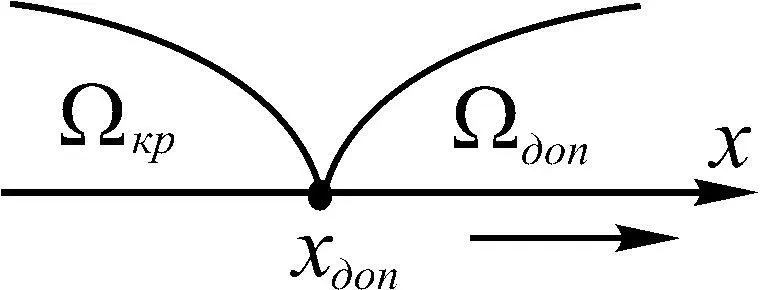
Рис. 1.22

3. Появление события А фиксируется подсистемой контроля или оценки в некоторый момент времени t в виде х o = х изм , представляющем собой событие D : ( x o < x доп ), где x o– оценка текущего (фактического) значения x ф ; x доп – ограничение одностороннее снизу.

4. При появлении события D в процессе принятия решения из-за ошибок, имеющих место в системе контроля, формирующей x o , опасное состояние динамической системы может не аннулироваться, а развиваться, т. е. наступает событие E : ( x ( t ) < x доп , t > τ).

5. Событие А реализуется на отрезке времени [ t 0, T ], на котором все события приняли безвозвратный характер. Это событие обозначим: С : ( x ( t ) < x доп , t [ t 0, T ]).

При этом вероятность P ос перехода динамической системы в опасное состояние записывается так:

P oс = P ( A, B, D, E, C ) = P ( A, B ) · P ( D, E,C / A, B ),

где P ( A, B ) – вероятность появления фактора риска, обусловливающего опасное состояние динамической системы; P ( D, E, C / A,B ) – условная вероятность пребывания динамической системы в критической области.

Представим P ( D, E,C / A, B ) и соответствующие ему ситуации в виде

P ( D, E, C / A, B ) = P ( D, E / A, B ) + P ( C / A, B )

в силу независимости ( D, E ) и ( С ).

Предполагая, что ошибки принятия решения и ошибки оценки, совершаемые динамической системой, есть независимые события, получим

P oс = P ( A, B )[ P ( D / A, B ) + P ( E / A, B ) + P ( C / A, B )].

При этом вероятность P ( D / A, B ) позволяет оценить наши возможности в области оценок (измерений) и допускаемых ошибок, которые влияют на процесс возникновения опасной ситуации.

Вероятность P ( E / A, B ) равна вероятности непарирования критических значений контролируемого параметра из-за ошибок управления.

Вероятность P ( C / A, B ) характеризует численно величину аварийной ситуации (катастрофы).

Таким образом, нижеследующие события характеризуют:

( А, В ) – усложнение функционирования динамической системы;

( А, В, D ) – опасную ситуацию;

( А, В, D, Е ), ( А, В, С ) – катастрофическую ситуацию.

При этом P ос является интегральной характеристикой риска динамической системы.

Исходной информацией при оценке P ос является область допустимых состояний Ω доп . Задача построения P ос включает в себя:

– обоснование совокупности параметров х состояния динамической системы, подлежащих контролю и ограничению;

– разработку математического метода количественного расчета фактических значений параметров х с заданной степенью достоверности;

– разработку методов оценки погрешностей измерения параметров х с заданной степенью достоверности;

– разработку математического метода расчета допустимых значений х , т. е. x доп .

Процессу целереализации соответствуют три уровня состояния динамической системы:

– допустимых состояний Ω доп ( х ), при которых динамическая система способна достичь поставленную цель, например, когда θ > 0, > 0;