Владимир Живетин - Введение в теорию риска (динамических систем)

Последняя предназначена для получения количественной информации о состоянии объекта исследования, обработки ее и выдачи потребителю. Следовательно, нужно рассматривать ее как средство получения информации в неразрывной связи с объектом исследования и потребителем. С помощью информационно-измерительных систем решается задача оценивания состояния системы путем обработки результатов измерений.

В системе контроля (подсистема 4) устанавливается соответствие между свойствами объекта контроля и заданной нормой, определяющей качественно различные области его состояния. При этом решаются следующие задачи:

– получение текущих значений контролируемых параметров x i 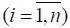, определяющих данное состояние объекта контроля;

– сопоставление текущего значения х i 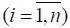и его допустимых значений ( x i ) доп , которые описывают область нормального состояния объекта контроля;

– получение и выдача результатов контроля, т. е. суждения о том, каково положение компонент х i вектора х относительно ( x i ) доп .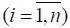

Отметим, что погрешности информационно-измерительных систем оказывают существенное влияние на результат контроля и, следовательно, создают предпосылки выхода параметров системы из допустимой области состояний.

Перечислим основные проблемы.

1. Есть динамическая система, она создана и подлежит изучению, моделированию, математическому описанию на структурно-функциональном уровне.

2. Для построения модели фактических значений процессов x ( t ), формируемых динамической системой, возможны измерения этих процессов, которые принимают значения в пространстве В 1фазовых координат динамической системы.

3. Измеренные значения процесса x ( t ) обозначим х изм – в общем случае случайные процессы или поля. Измеренным х изм значениям необходимо ставить в соответствие вероятностное пространство B 2= (Ω, f, P ). Для отображения В 1в В 2вводятся символические обозначения, интерпретирующие объекты как аналоги в этих пространствах [17];

4. Исследование модели в вероятностном пространстве, получение показателей, которые могут быть подтверждены, так, например, экспериментальным методом.

Сложность такого подхода обусловлена неадекватностью отображения пространства В 1в пространство В 2. Отметим, что вероятностное пространство служит базовой основой для [17]:

– вероятностных моделей;

– статистического моделирования;

– теории статистических решений.

В качестве вводных положений, необходимых в дальнейшем при применении теории вероятностей, используемой в теории риска динамических систем, приведем общее понимание теории вероятностей на структурном уровне [24].

Теория вероятностей как динамическая система знаний, синтезированная на структурно-функциональном уровне, представлена на рис. 1.25.

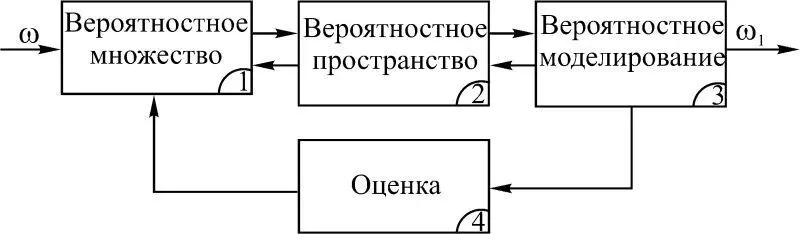
Рис. 1.25

Подсистема 1. Математическая статистика. Множества случайных величин. Вероятностное множество.

Подсистема 2. Теория вероятностей и случайных процессов. Вероятностное пространство. Основы создания математических моделей.

Подсистема 3. Математическое моделирование, средства и методы решения конкретных математических задач.

Подсистема 4. Оценка достоверности знаний. Математическая статистика. Погрешности.

Задача построения модели динамической системы формулируется следующим образом: по известным экспериментальным данным, полученным на выходе изучаемого объекта в виде множества исходов ω, необходимо создать модель М 1, формирующую множество исходов ω 1, близкое в некотором заданном смысле к ω.

Пусть мы нашли факторы ω на выходе изучаемого объекта, которым можем поставить в соответствие фактор ω 1на выходе подсистемы 3, тогда можем рассматривать статистические функции распределения F (ω) и F (ω 1).

Созданная модель М 1считается верной с точностью до (1–ε), если

|F (ω) – F (ω) 1) | < ε,

где ε – заданная величина.

Получен первичный критерий достоверности знаний, т. е. истинности модели М 1[55] в виде F (ω 1), формирующей множество ω 1.

Рассмотрим способ построения вероятностных или статистических моделей, используемых для описания исследуемых систем и объектов, обладающих энергетическо-информационным потенциалом. При формировании этих моделей используются алгоритмы, однозначно определяющие содержание и последовательность операций, переводящих совокупность исходных данных в искомый результат – цель исследования. Количество операций (действий) определяется степенью детализации изучаемых статистических и вероятностных моделей. Необходимость систематизации алгоритмов статистических решений обусловлена изобилием объектов и систем.

Задача состоит в том, чтобы подобрать научно обоснованные правила построения алгоритма и в результате получить компактно изложенные основы построения вероятностных моделей, охватывающие все возможное многообразие конкретных алгоритмов, вместо рассмотрения конкретного алгоритма для построения конкретной характеристики. При этом необходимо осуществлять как синтез искомого алгоритма, так и его анализ. Поскольку алгоритм состоит из системы последовательно выполняемых действий от измерения физических величин до выдачи готового результата статистических измерений, расчленение алгоритма на составные элементы начинается с декомпозиции синтезированного алгоритма.

Кроме того, сложность построения искомой вероятностной модели для описания реальных систем связана с разнообразием характеристик. Так, в качестве характеристики положения распределения можно рассматривать: математическое ожидание, медиану, квантили заданного порядка, моду, антимоду; в качестве характеристики рассеяния: среднее квадратическое отклонение, срединное отклонение, интерквартильную широту; в качестве характеристик связи: корреляционные и кумулянтные функции (коэффициенты) разных порядков, структурные и дисперсионные функции. Каждая из указанных характеристик имеет свои функциональные достоинства или недостатки. Эти характеристики должны отвечать цели и назначению изучаемой вероятностной или статистической модели.

Постановку и решение задачи необходимо осуществлять с системных позиций, когда исследуемый объект – система – включен в процесс исследования и построения моделей различного уровня. Для оценки возможностей построения стохастических математических моделей рассмотрим возможности применения алгоритмов обработки статистических данных. На рис. 1.26 представлены результаты структурно-функционального синтеза системы алгоритмов теории статистических решений.