Владимир Живетин - Введение в теорию риска (динамических систем)

– ресурсов ( v 1);

– государства с его законами и исполнительными органами ( v 2);

– общества, в том числе трудового коллектива, требующего от социально-экономической системы выполнения своих запросов ( v 3);

– космоса и окружающей среды, требующих вложения человеческих сил для обеспечения нормальной жизнедеятельности космоса ( v 4);

– культуры, создающей определенный интерес к другой жизни и другим взглядам на жизнь, желания изменить свою жизнь ( v 5);

– политики, без которой сегодняшнее общество не существует ( v 6);

– финансов, т. е. стимула для развития динамической системы ( v 7).

Каждое из этих управлений-возмущений непрерывно изменяется как во времени, так и в пространстве состояния динамической системы. Таким образом, Ω доп = Ω доп ( v ( v 1, …, v 7), Ω кр = Ω кр ( v 1, …, v 7).

С учетом сказанного, при оценке рисков и безопасных значений индикаторов динамической системы необходимо принимать во внимание следующее.

1. На вход динамической системы поступают ресурсы, а на выходе имеем совокупность параметров х ( t ), подлежащих контролю, ограничению и управлению.

2. Динамическая система предназначена для достижения заранее определенной цели, которая может меняться в процессе функционирования, в том числе по воле человека.

3. Невыполнение поставленной задачи означает потери создателя динамической системы и его риск.

4. Каждая динамическая система имеет множество критических состояний, в которых она теряет свои свойства и не способна выполнять поставленные задачи.

5. Потери, обусловленные недостижением цели, связаны с выходом контролируемых параметров в критическую область.

6. Область допустимых состояний Ω доп и соответствующие ей x доп изменяются в процессе функционирования и определяются экспериментально или теоретически.

7. Для предотвращения потерь и наилучшего достижения цели динамическая система должна включать в себя системы контроля и управления.

8. Система контроля обладает погрешностями, что обусловливает в процессе функционирования динамической системы необходимость строить область допустимых состояний Ω к доп . При этом, как правило, Ω доп и Ω к доп не совпадают, т. е. Ω к доп 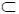Ω доп .

9. Оператор (человек), используя информационно-измерительную систему для управления, получает измеренные значения контролируемых параметров, которые обозначим x изм .

10. На выходе динамической системы реализуются фактические значения параметров, которые обозначим x ф . При этом x изм = x ф + δ х , где векторный случайный процесс δ х – погрешность информационно-измерительной системы.

11. Фактические значения параметров x ф , в силу объективных причин, обусловленных внешними возмущениями и внутренними шумами, а также субъективными причинами, свойствами управлений от человека, изменяющимися случайным образом, представляют собой случайные процессы. На этапе анализа динамической системы векторный процесс x ф должен задаваться с помощью математических моделей.

12. Для компенсации влияния δ х на величину риска вводятся такие допустимые при контроле значения x к доп и соответствующая им область Ω к доп 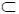Ω доп , которые в одномерном случае записываются в виде | x доп – x к доп | > 0, когда реализуется требование x доп ≠ x к доп .

13. При контроле над динамическими процессами, когда скорость изменения процесса во времени 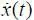≠ 0, необходимо вводить дополнительный запас, например, в виде 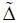= k | 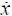| и вектор х дин доп = х доп ± 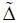. В результате имеем Ω к доп 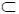Ω дин доп 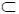Ω доп при двустороннем и одностороннем ограничении.

14. Предотвращение потерь состоит в обеспечении условия x ф ( t ) Ω доп ( t ) для любого момента времени t функционирования динамической системы. Для целей управления мы располагаем величиной x изм , кроме того, система контроля индуцирует не область Ω доп , а Ω к доп . При этом х к доп = х доп + δ х доп , где δ x доп – погрешность функционирования системы контроля, а x к доп задает границы Ω к доп . В этих условиях можно обеспечить только условие х изм Ω к доп , а это означает, что возможен выход x ф из области Ω доп , что может привести к соответствующим потерям и рискам.

15. В силу того, что процессы x ф и x изм являются случайными, в качестве меры риска будем рассматривать вероятности P событий, приводящие, например, к экономическим, техническим, финансовым и другим потерям.

16. С учетом сказанного, необходимо разработать показатели риска

P = P ( x доп , x дин доп , x к доп, М о k ( х ф ), М о k ( х изм ), a, b ),

где М о k ( х ф ) – центральный момент k- го порядка векторного случайного процесса x ф для всех k N; М о k ( х изм ) – центральный момент k -го порядка векторного случайного процесса x изм ; векторные величины a, b – параметры системы.

17. Полученные расчетным путем вероятности Р i 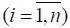уточняются в процессе функционирования динамической системы. В общем случае уточняются как P i , так и область Ω к доп .

Рассмотрим математическую модель вероятностных показателей риска и безопасности с учетом введенных понятий.

Поиск решения задачи в работе осуществляется при следующих допущениях относительно контролируемого и ограничиваемого индикатора x :

– критическое значение параметра состояния постоянно и не зависит от времени ( x кр = const);

– фактические и измеренные значения параметра представляют собой случайные процессы с известным законом распределения;

– превышение параметром (когда ограничение сверху) величины x кр на любом интервале времени ведет к критической ситуации.