Владимир Живетин - Введение в теорию риска (динамических систем)
- Название:Введение в теорию риска (динамических систем)
- Автор:
- Жанр:
- Издательство:Изд-во Института проблем риска, Информационно-издательский центр «Бон Анца»
- Год:2009
- Город:Москва
- ISBN:978-5-98664-052-5, 978-5-903140-63-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Живетин - Введение в теорию риска (динамических систем) краткое содержание
В работе вводятся первичные и вторичные показатель риска как для классических информационно-энергетических систем, так и для суперклассических – интеллектуально-энергетических систем.
Первичные показатели риска характеризуются множеством безопасных состояний, рассчитанных согласно, например, теории устойчивости; вторичные показатели риска представляют собой вероятности выхода динамической системы в область критических состояний с учетом свойств систем контроля и управления.
Полученные результаты позволяют осуществить математическое моделирование прогнозирования и управления рисками различных динамических систем, включая интеллектуально-энергетические.
Введение в теорию риска (динамических систем) - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
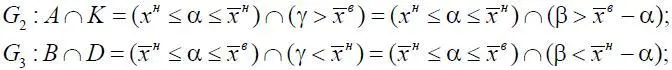
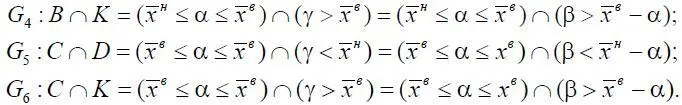
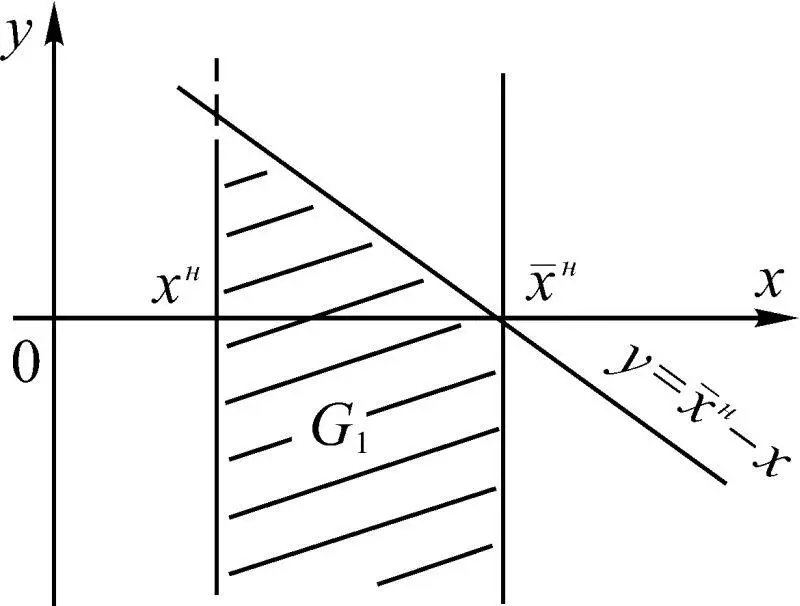
Рис. 1.42
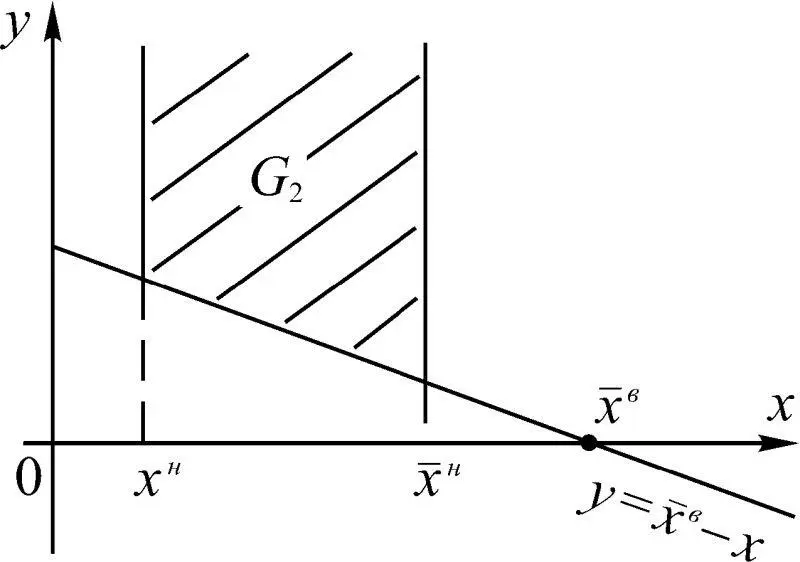
Рис. 1.43
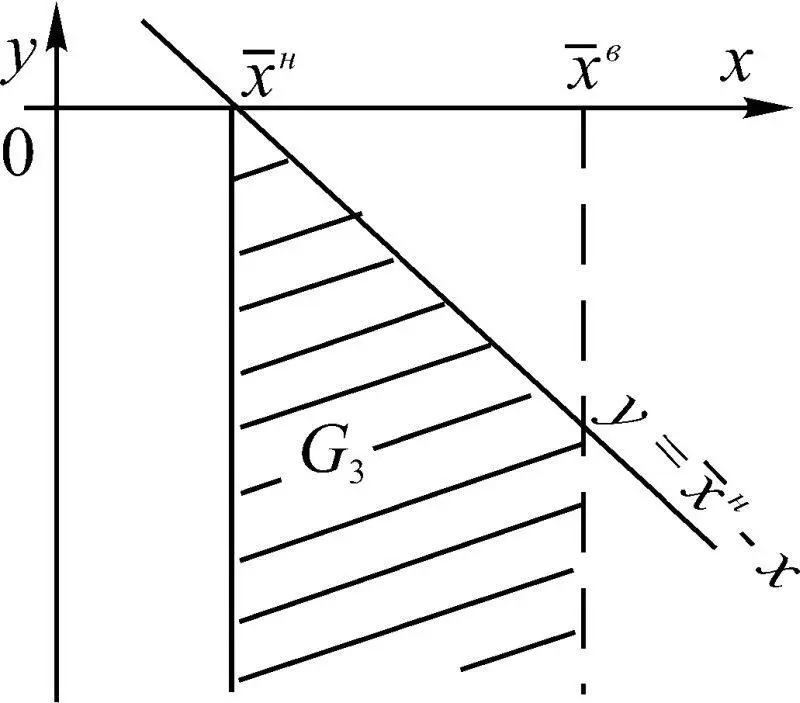
Рис. 1.44
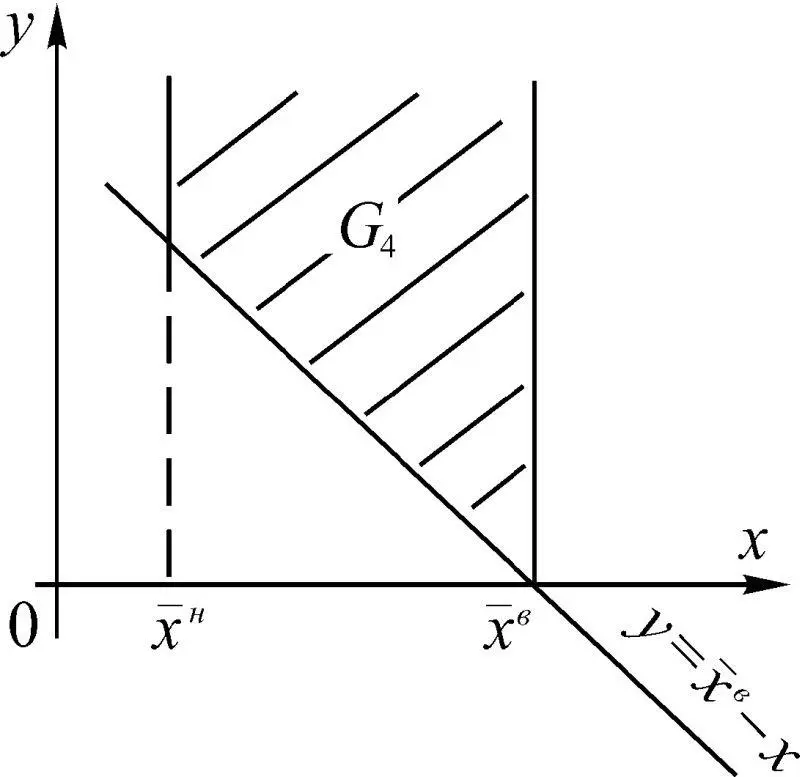
Рис. 1.45
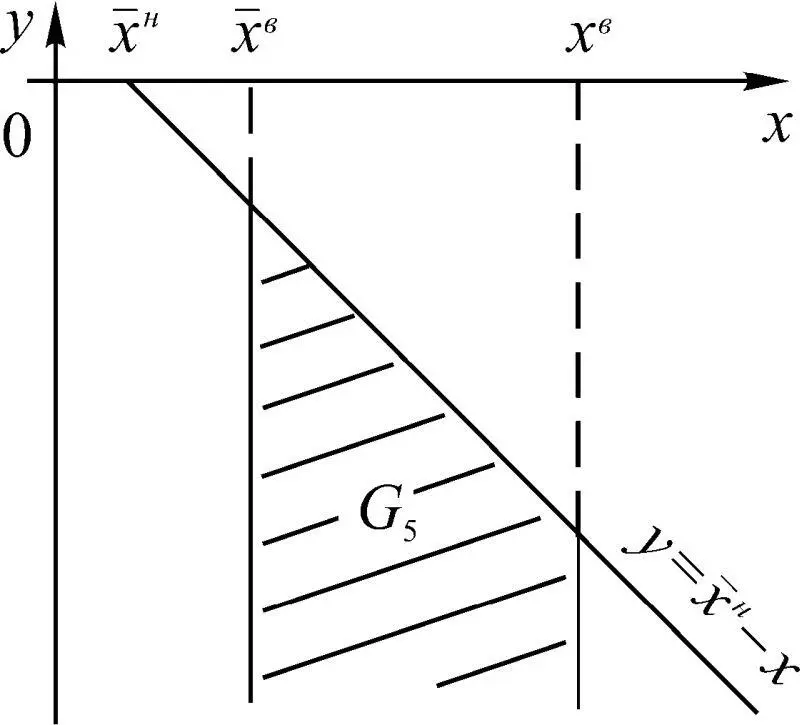
Рис. 1.46
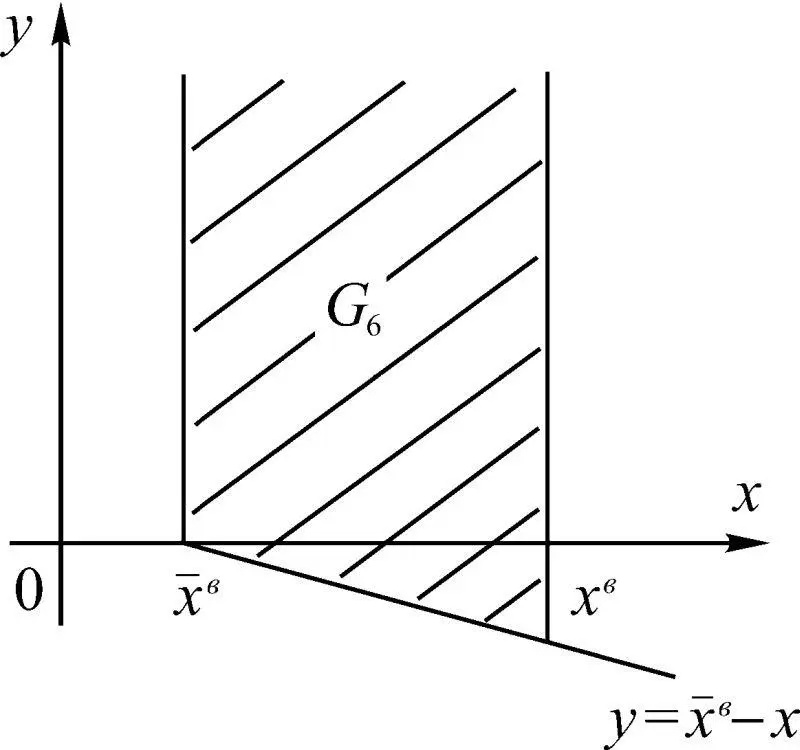
Рис. 1.47
Используя равенства (1.6), несовместность α и β, независимость А, В, С и несовместимость D, K , получим
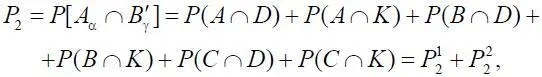
где
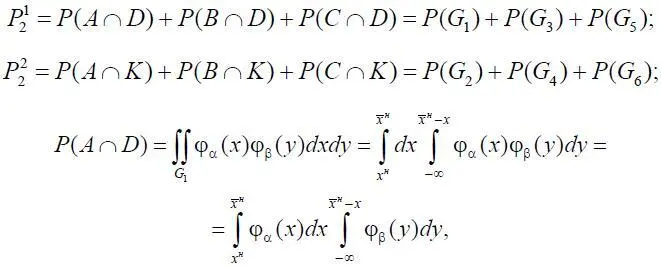
φ α( x ) – плотность вероятностей случайной величины α, φ β( y ) – плотность вероятностей случайной величины β;
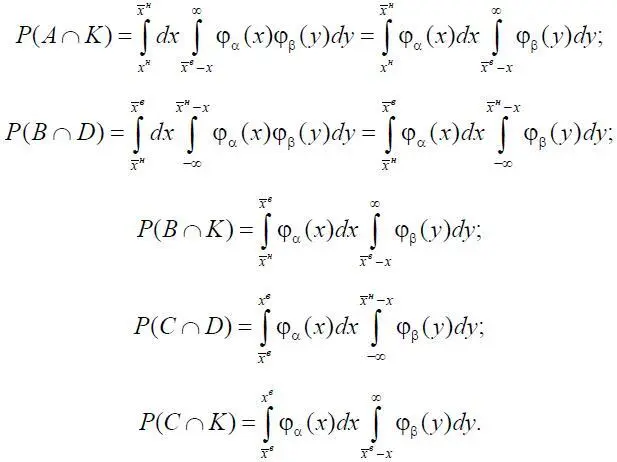
Таким образом, Р 2есть сумма двух вероятностей, одна из которых обусловлена событиями D , вторая – событиями K. Отметим, что полученное выражение справедливо для двустороннего ограничения индикатора х , подлежащего контролю и ограничению, когда измеренная величина х изм , с учетом погрешностей δ х , удовлетворяет D или K.
Окончательно,
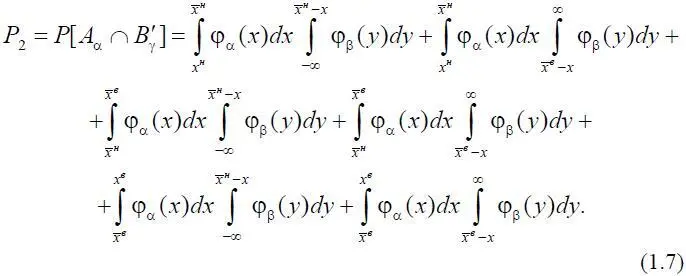
Из теории вероятностей известно, что
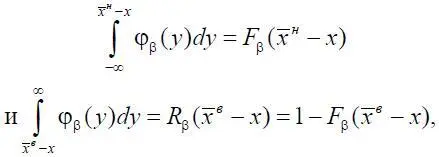
где F β( x ) – функция распределения случайной величины β; R β( x ) – дополнительная функция распределения случайной величины β. Тогда формулу (1.7) можно переписать в следующем виде:
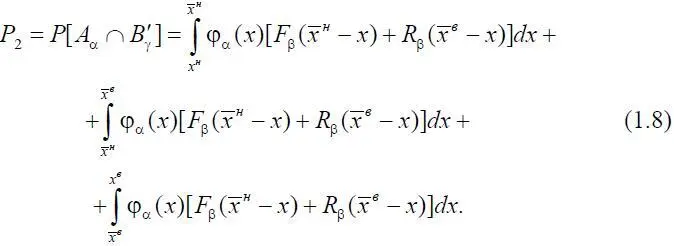
Перейдем к вычислению вероятности P 3:
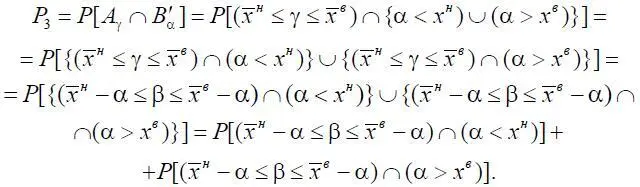
Таким образом,
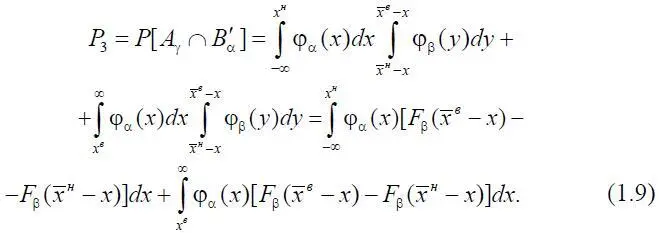
Если параметры подчинены односторонним ограничениям, то, согласно формулам (1.8) и (1.9), вероятности событий ( A α∩ B γ) и ( A γ∩ B' α) вычисляются следующим образом. В случае одностороннего ограничения сверху можно считать, что x н и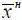 
→ ∞, тогда F β(–∞) = 0:
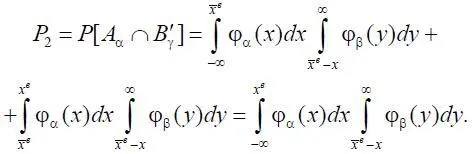
В случае одностороннего ограничения снизу можно считать, что x в ,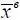 
→ +∞, и тогда
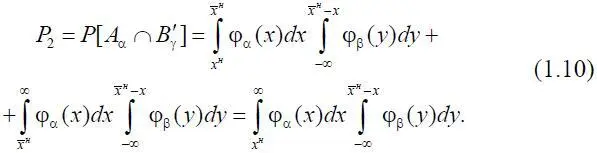
Аналогично, если x н , 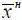→ +∞, то
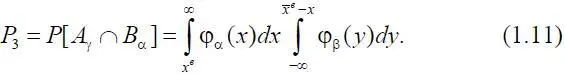
Если x в , 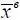→ +∞, то
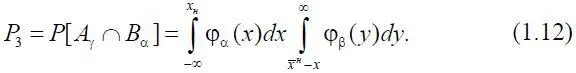
Часто при практических расчетах удобно использовать не φ α( x ), а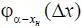 
, где Δ х = х ф – х н . В этом случае для индикатора, подлежащего ограничению снизу, получаем:
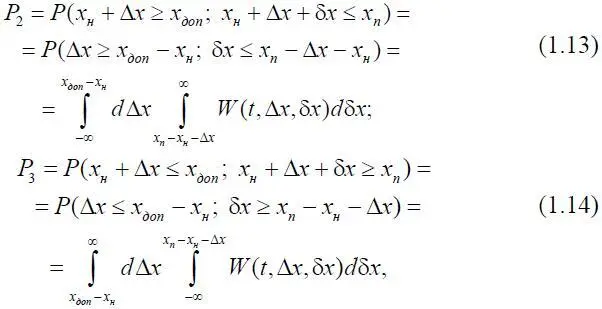
где W ( t, Δ x , δ x ) – совместная плотность распределения случайных процессов Δ x , δ x в момент времени t ; x n = x к доп.
Вид подынтегральной функции выражений (1.11), (1.12) либо (1.13), (1.14) и основные факторы, подлежащие учету при ее формировании, определяются объектами или подсистемами анализируемой системы и их режимом работы, а также множеством других параметров и факторов. При этом погрешность δ x , как правило, не оказывает влияния на величину отклонения от номинального режима Δ x . Это обстоятельство есть допущение, которое каждый раз необходимо проверять.
С учетом сказанного выше, при практических расчетах вероятностей P i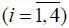 
зависимостью между погрешностями измерения δ x и величинами отклонения параметров Δ x от номинального режима можно пренебречь. В результате
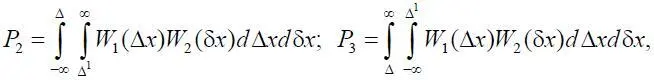
где Δ = x доп – x н ; Δ 1= x n – x н – Δ x.
На рис. 1.48 представлена геометрическая интерпретация событий, соответствующих вероятностям P 2и P 3, определяемым в случае, когда ограничение сверху.
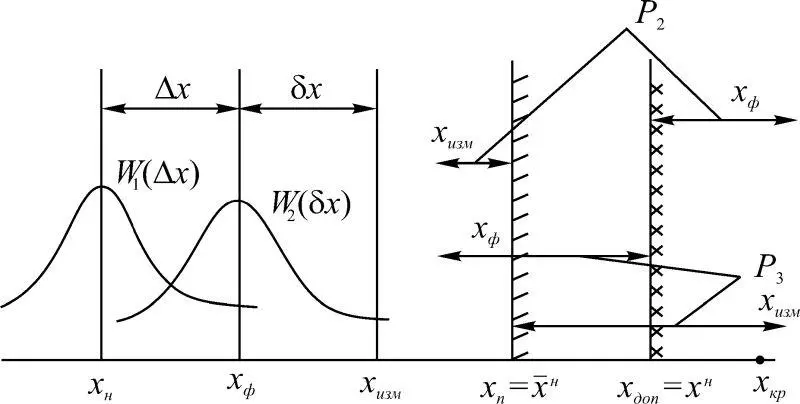
Рис. 1.48
Из последних соотношений следует, что вероятности Р 3и Р 2зависят от плотностей распределения W 1(Δ x ) отклонений x от номинальных значений x н , пороговых x n и допустимых x доп значений параметров, плотности распределения суммарной погрешности W 2(δ x ). В случае одностороннего ограничения Р 3представляет вероятность попадания точки (Δ x , δ x ) в область G 1, ограниченную прямыми Δ x = а = x доп – x н и δ x = x n – x н – Δ x (рис. 1.49). Величина δ x изменяется от –∞ до b = x n – x н . Вероятность попадания точки (Δ x , δ x ) в область G 2представляет собой Р 2.
Случай двустороннего ограничения параметров представлен на рис. 1.50. При этом Р 3представляет вероятность попадания точки с координатами (Δ x , δ x ) в области G 1и G 3одновременно, а вероятность Р 2 – попадание (Δ x , δ x ) в области G 2, G 4одновременно.
Читать дальшеИнтервал:
Закладка:
