Владимир Живетин - Введение в теорию риска (динамических систем)

2) вероятности Р 21= Р ( S 21) = Р ( А α∩ С γ) и Р 22= Р ( S 22) = Р ( А α∩ В γ) – когда значение х ф находится в допустимой области, а система контроля фиксирует недопустимое значение;

3) вероятности Р 31= Р ( S 31) = Р ( С α∩ А γ) и Р 32= Р ( S 32) = Р ( В α∩ А γ) – значение х ф находится вне допустимой области, но система контроля подает сигнал о допустимом состоянии объекта;

4) вероятности Р 41= Р ( S 41) = Р ( С α∩ С γ) и Р 42= Р ( S 42) = Р ( В α∩ В γ) – значение х ф находится вне области допустимых состояний, одновременно система контроля подтверждает это состояние;

5) вероятности Р 51= Р ( S 51) = Р ( С α∩ В γ) и Р 52= Р ( S 52) = Р ( В α∩ С γ) – значение х ф находится вне области допустимых состояний, например по минимуму (максимуму), а система контроля показывает, что объект находится в недопустимой области, но с противоположной стороны – максимальной (минимальной).

Совокупность Р ij ( 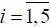; j = 1,2) образует полную группу несовместных событий, т. е. .

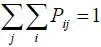Событие ( А α∩ А γ) соответствует правильному анализу состояния системы, а вероятность Р 11характеризует безопасное ее состояние, при котором осуществляется основная цель динамической системы. Если же осуществляются такой контроль и управление, при которых наступают события S 21, S 22, S 31, S 32, S 41, S 42, S 51, S 52, то цель, поставленная перед управляющей системой, не выполняется, так как возникают неоправданные (лишние) затраты потенциала θ = ( E,J,m ) по управлению. Эти состояния характеризуются потерями и называются опасными.

В качестве основных интегральных характеристик невыполнения цели, т. е. риска, будем рассматривать вероятности событий ( S 21, S 22), ( S 31, S 32), ( S 41, S 42), ( S 51, S 52):

Р 2= Р ( S 21 S 22) = Р ( S 21) + Р ( S 22),

Р 3= Р ( S 31 S 32) = Р ( S 31) + Р ( S 32),

Р 4= Р ( S 41 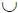S 42) = Р ( S 41) + Р ( S 42),

Р 5= Р ( S 51 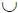S 52) = Р ( S 51) + Р ( S 52).

В дальнейшем из рассмотрения можно исключить ситуации, характеризуемые вероятностью Р 4, когда система контроля нам указывает на критическую ситуацию, но мы не имеем в своем распоряжении управления, способного возвратить в область безопасных состояний.

Система контроля, для которой события S 51или S 52теоретически осуществимы, порождает измеренные случайные величины или процессы, когда х ф находится в области ( х ф < 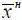), а измеренное значение х изм – в области ( х изм > 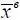) (рис. 1.41, здесь φ( ·) – плотность распределения) или наоборот.

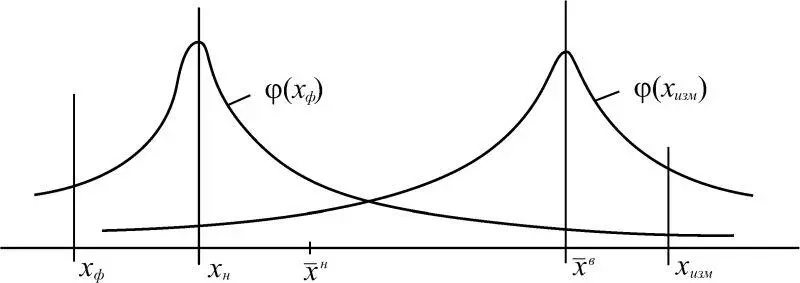
Рис. 1.41

Если учитывать физическую нереализуемость такого контроля, то события S 51и S 52невозможны.

На примере вероятностей Р 2, Р 3, которые наиболее важны при оценке риска динамической системы, рассмотрим построение математической модели, позволяющей получить численную оценку вероятностей Р 2и Р 3. Для вероятностей Р 1, Р 4, Р 5все выводы аналогичны и не представляют труда.

В качестве основных интегральных характеристик невыполнения цели будем рассматривать величины вероятностей событий ( А α∩ В' γ), ( B ' α∩ A γ):

P 2= P ( A α∩ B ' γ) = P ( A α) Р ( B' γ| A α);

P 3= P ( B' α∩ A γ) = P ( B' α) Р ( A γ| В ' α),

где В ' = ( B γ 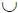С γ), В ' α= ( C 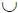α B α).

Вероятность Р 2характеризует появление ложной информации, поэтому назовем ее вероятностью ложной оценки состояния, а Р ( В' γ | А α) = Р' 2 – условной вероятностью ложной оценки состояния.

Вероятность Р 3характеризует такое состояние, при котором превышение х значения х кр не фиксируется в процессе контроля или оценки параметра х . Эту вероятность назовем вероятностью опасной ситуации , а P ( A γ| В' α) = Р' 3 – условной вероятностью опасной ситуации. Вероятности Р 2и Р 3включают Р' 2, Р' 3, которые не зависят от характеристик средств оценки или контроля и поэтому при анализе и синтезе системы контроля могут не рассматриваться. Однако это необходимо учитывать при назначении допустимых значений Р 2, Р 3, Р' 2, Р' 3. При этом Р 2и Р 3отличаются от Р' 2, Р' 3на постоянные величины.

Запишем вероятности Р 2и Р 3в явном виде и выразим их через x н, x в , 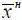, 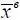и плотности распределения вероятностей случайных величин α и γ. Вероятность

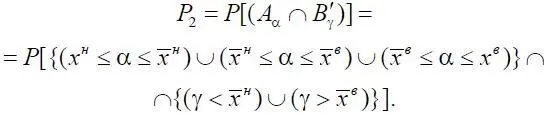
Воспользуемся дистрибутивными свойствами символов ∩ и . Обозначим

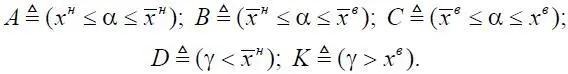
Тогда для Р 2имеем:

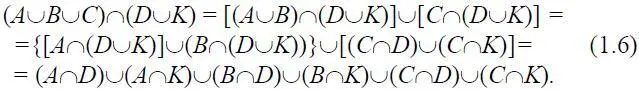
Рассмотрим каждое из пересечений отдельно. Рассмотрим область на плоскости:

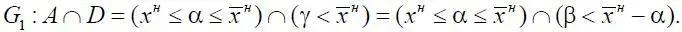
Так как α и β – случайные независимые величины, то область их значений можно изобразить так. Обозначая реализацию α через x , а реализацию β – через y , получим ситуацию, изображенную на рис. 1.42 в виде области G 1. Аналогично рис. 1.43–1.47: