Владимир Живетин - Введение в теорию риска (динамических систем)

Введем необходимые обозначения.

Текущее , или фактическое , значение параметра запишем в виде x ф = x н + Δ x , где x н – номинальное значение (математическое ожидание) параметра; Δ x – отклонение параметра движения x относительно x н . Обозначим через δ x погрешность измерения параметра. Тогда измеренная величина параметра контроля x будет определяться суммой:

x изм = x н + Δ x + δ x.

Обозначим α 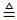x н + Δ x = х ф ; β 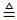δ x ; γ 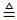x изм = α + β ( 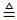означает равенство по определению); x в доп 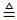x в , x н доп 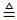x н – соответственно верхнее и нижнее допустимые значения х ф ; x кв доп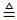 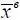, x кн доп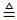 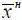– для измеренных значений x верхнее и нижнее допустимые соответственно; x н < 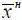< < 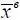x в (рис. 1.35).

Очевидно, что по известным вероятностным характеристикам (Δ x , δ x, x изм ) находятся вероятностные характеристики (α, β, γ) и наоборот. При этом рассматривается вектор (α,γ) зависимых случайных процессов, в частности стационарных, а α и β – независимые случайные процессы (величины).

В процессе выполнения поставленной цели относительно фактических и измеренных значений возможны следующие события.

1. Фактическое значение α параметра находится в области допустимых значений, т. е. на одном из трех отрезков, принадлежащих промежутку [ x н , х в ] (рис. 1.35). Тогда имеем событие А α 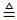{( x н ≤ 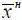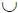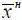α ≤ ) ( ≤ α ≤ 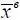) 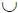( 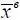≤ α ≤ х в )}.

2. Фактическое значение α находится вне области допустимых состояний, превышая х в (рис. 1.36). В итоге имеем В α 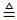{α > х в }.

3. Фактическое значение α находится вне области допустимых состояний, не достигая х н (рис. 1.37). В итоге имеем C α 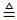{α ≤ х н }.

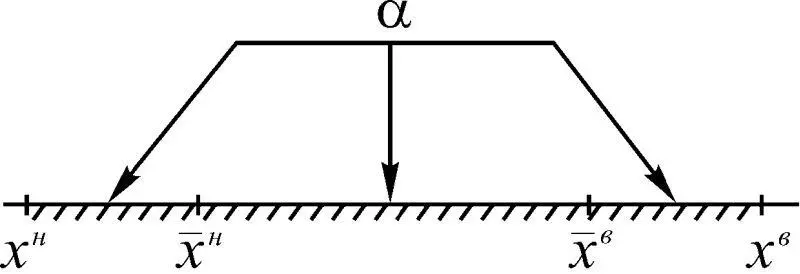
Рис. 1.35

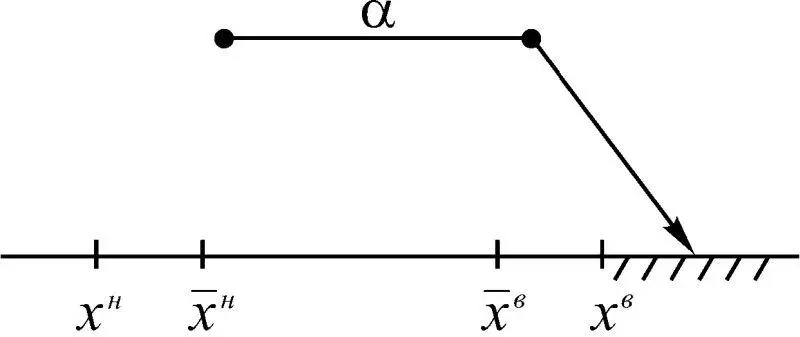
Рис. 1.36

4. Измеренное значение γ индикатора х состояния динамической находится в области допустимых состояний объекта (рис. 1.38). В этом случае имеем событие A 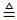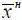γ { ≤ γ ≤ }.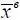

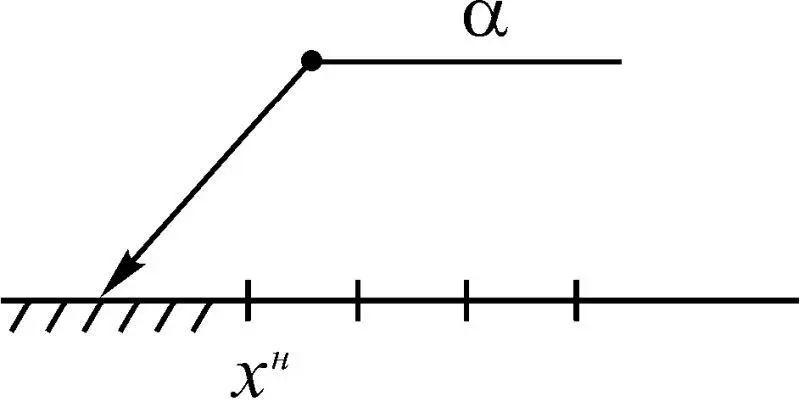
Рис. 1.37

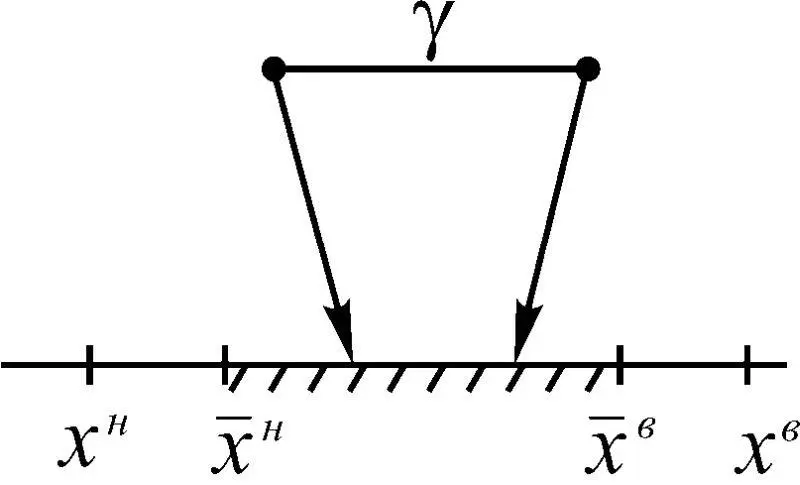
Рис. 1.38

5. Измеренное значение γ индикатора х состояния динамической системы находится вне области допустимых значений, превышая 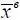(рис. 1.39). В итоге имеем В 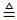γ {γ ≥ }.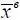

6. Измеренное значение γ индикатора х находится вне области допустимых значений, не достигая 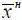(рис. 1.40). В итоге имеем С 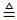γ {(γ ≤ )}.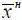

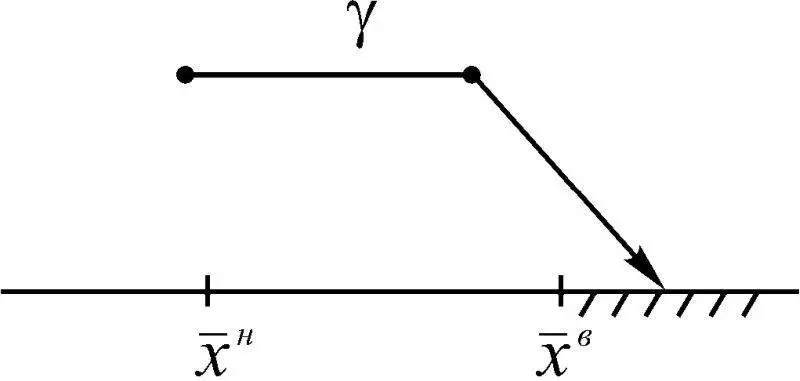
Рис. 1.39

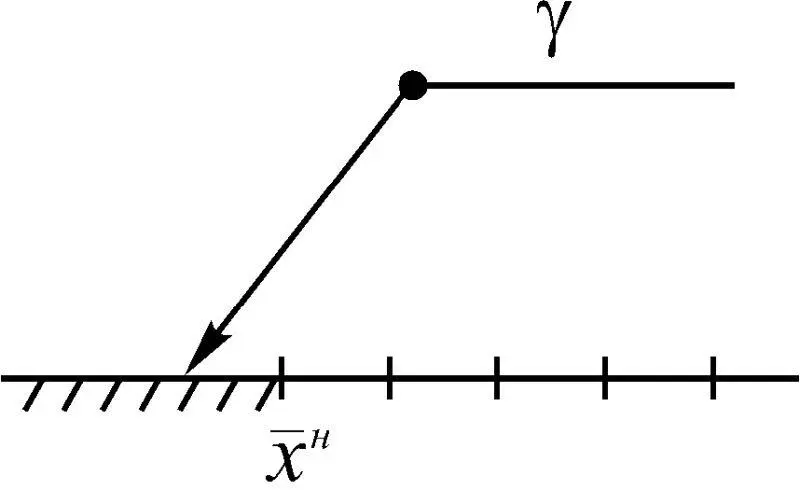
Рис. 1.40

В процессе контроля индикатора х , изменяющегося во времени на всей числовой оси, возможны следующие гипотезы.

Гипотеза А α . Ограничиваемый индикатор х , его фактическое значение х ф , находится в области допустимых значений, т. е. имеет место событие А α.

Гипотеза В α . Фактическое значение индикатора динамической системы x ф находится вне области допустимых состояний B α. С помощью средств контроля или оценки имеем А γ, В γили С γ.

Гипотеза С α . Фактическое значение индикатора динамической системы x ф находится вне области допустимых состояний С α. С помощью средств контроля или оценки имеем А γ, В γили С γ.

В итоге имеем различные события S ij , которые сгруппируем следующим образом:

I. ( А α∩ А γ); → S 11;

II. ( А α∩ С γ); ( А α∩ В γ); → S 21, S 22;

III. ( С α∩ А γ); ( В α∩ А γ); → S 31, S 32;

IV. ( С α∩ С γ); ( В α∩ В γ); → S 41, S 42;

V. ( С α∩ В γ); ( В α∩ С γ); → S 51, S 52.

Полученные события характеризуют следующие контролируемые состояния динамической системы:

I) безопасные (в норме);

II) опасное ложное из-за ошибок измерения (фактическое безопасное);

III) опасное (пропуск со стороны системы контроля);

IV) опасное известное (форс-мажор);

V) опасное известное – нонсенс (несообразность), вероятность которого пренебрежимо мала.

Каждое из событий S ij характеризуется соответствующей вероятностью:

1) вероятность Р 11= Р ( S 11) = Р ( А α∩ А γ) – когда поступает информация о допустимом состоянии х , и фактическое его значение х ф допустимо;