Владимир Живетин - Системные человеческие джунгли рисков

Положим, что τ D = const, что существенно упрощает модель, превращая ее в линейную. Тогда мы получим 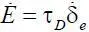. При этом (1.1) запишется в виде

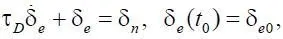
где δ e 0= E 0/ τ D – начальное значение δ e ( t ) при t = t 0.

В полученном уравнении τ D характеризует инерционное запаздывание потока расходов δ e по отношению к потоку поступления δ n . Введение инерционного запаздывания τ D в динамической системе означает параметризацию процесса, когда сложная функциональная зависимость между расходами δ e и имеющимися средствами E ( t ) сводится к одному параметру τ D . Зависимость τ D от u 2при τ D = const из функциональной превратилась в числовую. Однако если состояние социальной системы и подсистем изменяется, то это необходимо учитывать в лучшем случае в виде τ D = τ D ( t ), а в более трудном – в виде τ D = τ D ( u 2). Для установившихся процессов τ D является постоянной величиной, характеризующей данную динамическую систему и социальную систему, в которой она функционирует.

Чистое запаздывание аргумента τ в уравнении (1.3) существенно затрудняет процесс анализа. Для упрощения модели заменим чистое запаздывание инерционным запаздыванием. Представим (1.3) в виде

δ n ( t ) = δ (1) e ( t – τ)[1 + p* ( t – τ)],

где p* ( t – τ) = τ p ( t – τ)/(360·100); τ = const.

Введя обозначение s = t – τ, получим

δ n ( s + τ) = δ (1) e ( s )[1 + p* ( s )]. (1.5)

Разложив δ n ( s + τ) по степеням τ и оставив члены только первого порядка, получим

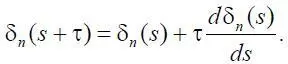
Подставив последнее выражение в (1.5) и в силу произвольности s заменив его на символ t , получим

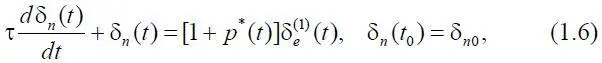
где δ n 0– начальное значение δ n ( t ).

Величина δ ( 2) e ( t ) расхода энергии в (1.2) во внутренней среде динамической системы состоит из ряда слагаемых, которые представим в форме:

δ (2,1) e ( t ) = γ 1δ e ( t ); δ (2,2) e ( t ) = γ 2δ e ( t );

δ ( е 2, 3)( t ) = γ 3δ e ( t ); δ (2,4) e ( t ) = γ 4δ e ( t ),

где γ 1, γ 2, γ 3, γ 4определяют доли, которые составляют от δ e потоки δ ( 2, i ) 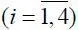соответственно. Следовательно,

δ (2) e = γδ e ,

где γ = γ 1+ γ 2+ γ 3+ γ 4.

Часть δ e , равная δ (1) e = (1 – γ)δ e , идет в социальную систему для создания энергетического потенциала δ n ( t ). Поэтому неравенство δ (1) e > 0 будет характеризовать энергообеспеченность динамической системы, поскольку величина δ (1) e представляет энергетический поток, направленный в социальную систему. Кроме того, из соотношения δ (1) e = (1 – γ)δ e > 0 следует неравенство δ e > 0 и γ < 1, что также представляет условие энергообеспеченности динамической системы (общества или человека).

С учетом принятых допущений система (1.1)–(1.3) примет вид

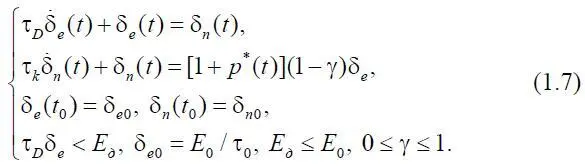
Введением τ k вместо τ мы уточняем модель, обусловленную погрешностью перехода от чистого запаздывания τ к инерционному. При этом между ними имеет место приближенное равенство

τ ≈ 3τ k , (1.8)

которое следует из условия вхождения решения уравнения (1.6) в 5-процентную «трубку», т. е. совпадение решений уравнений при чистом и инерционном запаздываниях с точностью не менее 5 %.

Система уравнений (1.7) является замкнутой относительно δ e и δ n . Управлением служит параметр γ, определяющий долю затраченной энергии, кроме той, что идет в социальную систему.

В систему (1.7) входят параметры τ D , τ k, p *, γ и другие условия, в том числе начальные. При этом p* и γ так или иначе задаются, т. е. являются управляемыми, а два параметра τ D , τ k отражают свойства самой динамической системы, и их следует идентифицировать.

В общем случае необходимо учитывать потоки , формируемые для погашения вложений «инвестора». В качестве инвестора выступает любая динамическая система из социальной системы А 2, способная передать часть своего ресурсного потенциала θ( t 0) в форме кредитных потоков .

Поток 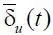в некоторой мере управляем со стороны системы А 1, ибо не все вложения со стороны «инвесторов» необходимы для максимизации процессов целереализации. Возможно, что условия, на которых предлагаются вложения «инвесторов», невозможно выполнить. Поток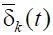и и 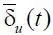определяются на основании решения системы и формируются в моменты времени t k = (t – 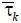) и t u = (t – 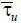). При этом имеют место соотношения

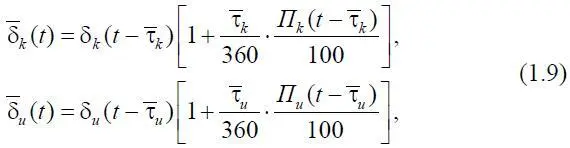
где П k (t – 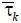) и П u (t – 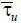) – проценты, характеризующие возможности динамических систем, отдающих θ и получающих θ, в момент времени (t – 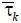) и (t – ).

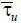Кроме сказанного в некоторых случаях следует рассматривать Е = ( Е м , Е ин ), где Е задано уравнением (1.1); Е м – материальная компонента; Е ин – интеллектуальная компонента динамической системы.

Уравнения (1.7)–(1.9) представляют собой математическую модель материальной компоненты системы, т. е. подсистемы (3). Функционирование подсистем (1, 2, 4) системы, создающее управления подсистемой (3) и соответствующими процессами 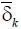, , 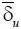обеспечивается трудовым и творческим потенциалами, формируемыми из состава общества. Каждый человек обладает интеллектуально-энергетическим потенциалом θ ин , который изменяется во времени под влиянием внешних и внутренних факторов. Заполнив подсистемы (1, 2, 4) людьми с интеллектуально-энергетическим потенциалом различного уровня, мы получим различные управления, которые сформируют различный материально-энергетический потенциал Е м в подсистеме (3) динамической системы. При этом изменение Е м и Е ин во времени описывается системой нелинейных уравнений вида: