Владимир Живетин - Системные человеческие джунгли рисков

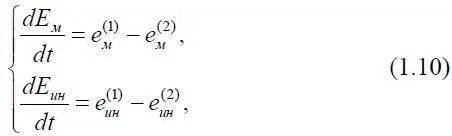
где Е м , Е ин – материальная и интеллектуально-энергетические компоненты; полная энергия динамической системы Е дс = ( Е м , Е ин ) ; е (1) м , е (1) ин – входные потоки энергии материального и интеллектуально-энергетического; е ( 2 ) м , е ( 2 ) ин – выходные компоненты энергетических потоков.

В системе (1.10) материальный поток е ( 2 ) м ( t ) зависит от коэффициента функциональных затрат K ( t ), т. е. е ( 2 ) м ( t ) = е ( 2 ) м ( K ( t ), t ). Коэффициент K ( t ) зависит от интеллектуально-энергетического потенциала людей, наполняющих подсистемы (1–4), т. е. K ( t ) = K ( E ин, t ). При некоторых значениях E ин ( t ) коэффициент K ( t ) достигает критического значения 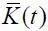, и тогда Ė м < 0, т. е. материальный потенциал системы падает. Возможность восстановления такого состояния динамической системы, при котором Ė м > 0, когда K (t) > 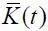(ограничение было снизу, а e (2) м возрастает по K ( t )), зависит от времени τ пребывания K ( t ) в критической области. При некотором τ* реализуется значение E м < ( E м ) кр , где ( E м ) кр – критическое значение Е м , при котором система неспособна реализовать поставленную цель.

Решение полученной нелинейной системы дифференциальных уравнений возможно численными методами.

Найдем стационарное решение системы (1.7), когда δ n и δ e – постоянные величины. Из уравнений (1.7) при 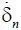= 0, 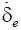= 0 следует, что возможности (расход) всегда будут равняться потребностям (поступлениям), если имеет место равенство

(1 – γ)(1 + р* ) = 1. (111)

При этом доля расходов γ удовлетворяет условию

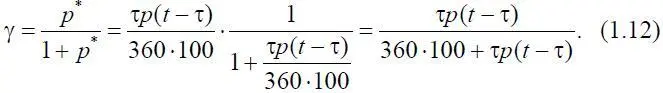
Таким образом, обобщенным параметром, определяющим допустимые расходы, выступает произведение τ р. График зависимости (1.12) представлен на рис. 1.20. Если γ принадлежит кривой γ = f (τ p ), то количество отданного энергетическо-информационного потенциала θ равно количеству полученного θ. В случае когда γ не принадлежит кривой, нарушается баланс, и динамическая система либо развивается, либо деградирует. Рассмотрим это на режиме возмущенного движения для процесса δ e ( t ), изменение которого задано первым уравнением системы (1.7).

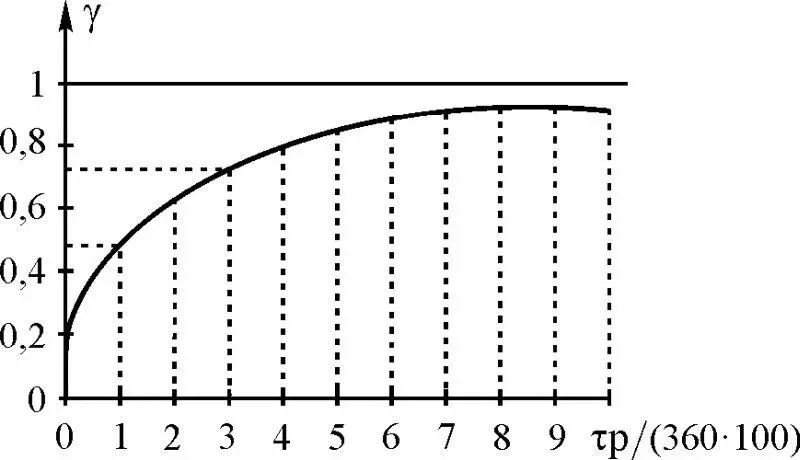
Рис. 1.20

Исключив δ n ( t ) из системы (1.7), получим одно дифференциальное уравнение второго порядка относительно δ e ( t ):

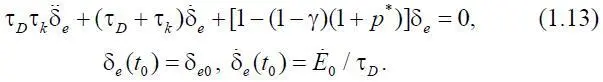
После того как построен процесс δ e ( t ) согласно уравнению (1.13), неизвестный процесс δ n ( t ) может быть определен из первого уравнения (1.7). Если коэффициенты уравнения (1.13) постоянны, то, используя известные методы, получим его аналитическое решение. Для этого запишем характеристическое уравнение

τ D τ k λ 2+ (τ D + τ k )λ + [1 – (1 – γ)(1 + p* )] = 0, (1.14)

решение которого имеет вид

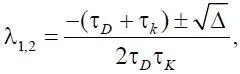
где Δ = (τ D + τ k ) 2– 4τ D τ k [1 – (1 – γ)(1 + p *)].

Если равенство (1.11) не выполняется, то в зависимости от величины и знака детерминанта δ корни λ 2будут вещественными или комплексными.

Введем обозначение

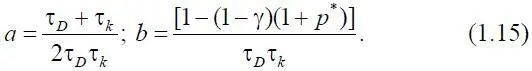
При этом

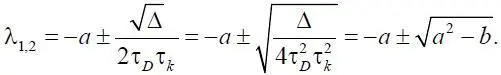
Величина а 2 всегда положительна. Положительна также и а в силу того, что τ D > 0, τ k > 0. Если τ D < 0 и τ k < 0, то рассматриваются динамические системы не с запаздывающим аргументом, а с опережающим, а это нонсенс (не может быть).

Величина b может быть как положительной, так и отрицательной. В зависимости от соотношения а 2 и b дискриминант δ может иметь разный знак.

При этом возможны следующие варианты.

Вариант 1.Случай, когда a 2 > b , дискриминант Δ > 0 и оба корня λ 1,2вещественные. В этом случае общее решение уравнения (1.13) имеет вид

δ e ( t ) = exp(– at ){1/2 · ( c 1+ c 2)exp( ct ) + 1/2 · ( c 1– c 2)exp(– ct )}, (1.16)

где .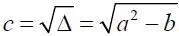

Постоянные с 1и с 2зависят от начальных данных δ е 0и 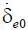и параметров системы следующим образом:

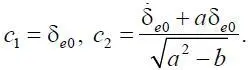
Анализ поведения динамической системы начнем со случая b = 0, соответствующего равновесному состоянию рассматриваемой системы. При этом выполняется условие (1.11) и Δ = a 2 , когда имеет место λ 12= – a ± a , т. е. λ 1= 0, λ 2= – 2a.

Общее решение (1.16) примет вид

δ e ( t ) = ( c 1+ c 2) / 2 + ( c 1– c 2) / 2 · exp(–2 at ),

где c 1= δ e 0, c 2= 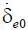/ a + δ e 0.

Из последнего равенства следует: равновесное состояние δ e = ( c 1+ c 2)/2 реализуется при любом значении t , если имеет место равенство c 1= c 2. Если c 1≠ c 2, то в силу того, что a > 0, такое состояние реализуется при больших значениях t , когда

δ e ≠ ( c 1+ c 2)/2.

При t → +∞ условие δ e = ( c 1+ c 2) / 2 соблюдается независимо от значений c 1и c 2(рис. 1.21).

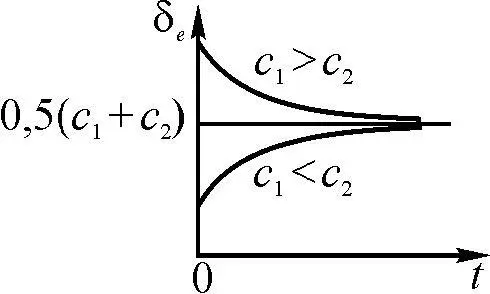
Рис. 1.21

Таким образом, состояние динамической системы, когда δ e = ( c 1+ c 2) / 2, обладает устойчивостью энергетических потоков на входе в динамическую систему и на О t выходе из нее по отношению к начальным возмущениям. При этом независимо от того, какое из неравенств – δ e (0) > ( c 1+ c 2) / 2 или δ e (0) < ( c 1+ c 2) / 2 – имело место, с увеличением t соотношение (1.16) становится более точным.