Виталий Скляр - Организация и математическое планирование эксперимента. Учебное пособие

Полученные в результате измерений значения случайной величины распределяются по определенному закону. Закон распределения случайной величины устанавливает связь между полученными значениями случайной величины и вероятностями их появления. Вид этого закона распределения является одной из характеристик случайной величины.

Допустим произведено n измерений случайной величины X и получены значения х 1, х 2 … х n. При этом если речь идет о дискретной случайной величине, то она примет определенные значения случайное число раз, обозначим это число m. Если речь идет о непрерывной случайной величине, то весь диапазон ее изменения разбивается на несколько интервалов и подсчитывается количество попаданий в каждый из интервалов. Вероятность того что дискретная величина примет какое-либо значение (или попадет в определенный интервал) в этом случае будет:

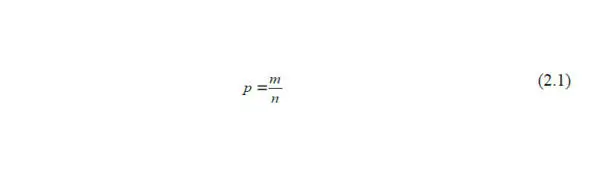
где m – число наблюдений, в которых дискретная случайная величина X оказалась равна x; n – общее количество наблюдений.

Сумма вероятностей всех возможных значений дискретной случайной величины (или попаданий во все интервалы для непрерывной) равна единице.

Для оценки распределения случайной величины используют функцию распределения и плотность распределения.

Функция распределения F (x) – это интегральная функция, которая показывает вероятность того, что случайная величина Х принимает значение не больше, чем х :

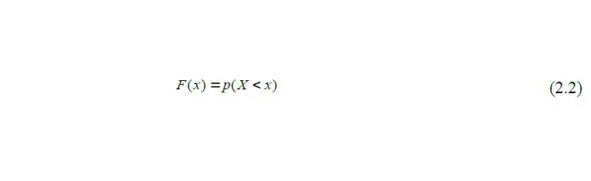
Функция распределения должна иметь возрастающий характер.

Плотность распределения f (x) – это дифференциальная функция – производная функции распределения, которая определяется как:

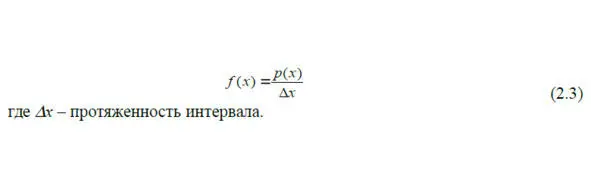
Для правильной обработки экспериментальных данных необходимо знать закон распределения, однако для его точного определения необходимо обработать большой объем экспериментальной информации.

Пример. На предприятии выпускается проволока различных диаметров. Отдел товарного контроля производит периодические замеры диаметра готовой проволоки. Результаты измерения (всего 50) проволоки диаметром 3,6 мм находятся в таблице 2.1. Значения диаметра проволоки отличаются друг от друга из-за того, что проволока производится в пределах допусков и диаметр может отличаться как в большую, так и в меньшую сторону и это не является нарушением технологии, также на результаты может влиять погрешность измерений.

Таблица 2.1 – Результаты замеров

Дальнейшую обработку данных ведем по следующей методике.

Для удобства необходимо отсортировать данные по порядку от большего к меньшему – таблица 2.2.

Для непрерывной случайной величины задают вероятность ее попадания в один из заданных интервалов области ее определения (поскольку вероятность того, что она примет какое-либо конкретное свое значение, стремится к нулю).

Таблица 2.2 – Упорядоченная таблица результатов замеров

Количество интервалов определяют по формуле

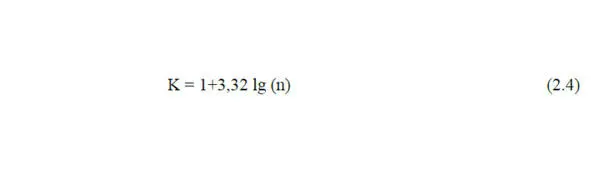
где n – количество измерений.

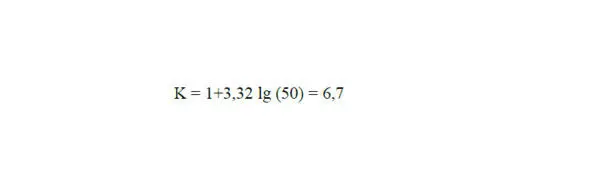
В качестве количества интервалов принимаем большее нечетное число – 7.

По таблице 2.2 определяем наибольшее и наименьшее значение х min= 3,4, х max= 3,8, диапазон изменений (размах) случайной величины L x= 3,8 – 3,4 = 0,4. Тогда продолжительность каждого из семи интервалов Δх = 0,4/7 = 0,057. Значение продолжительности интервала достаточно округлить на порядок больший, чем точность измерений случайной величины.

Таким образом, получим семь интервалов, границы которых приведены в таблице 2.3.

Теперь подсчитаем сколько раз случайная величина попала в каждый из интервалов, обозначим это значение – m, и частотную вероятность попадания в каждый интервал по формуле 2.1.

Например в интервал 3,4…3,457 попадает всего два значения из таблицы 2.2 – это 3,4 и 3,45, частотная вероятность в этом случае будет: р = 2/50 = 0,04, результаты для остальных интервалов приведены в таблице 2.3. Сумма всех вероятностей должна быть равна единице.

Для построения функции распределения необходимо определить сумму всех вероятностей с начала интервала до требуемого значения. Т.е. ее значение для второго интервала 0,04+0,08 = 0,12, для третьего 0,04+0,08+0,14 = 0,26 и т. д. Последнее значение всегда должно быть равно 1. График интегрального закона распределения (функции распределения) приведен на рисунке 2.1.

Таблица 2.3 – Данные для определения вида закона распределения

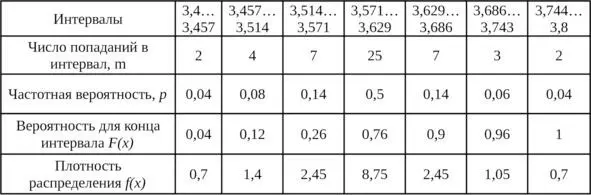
По формуле (2.3) рассчитываем плотность распределения для каждого из интервалов. Например для первого она равна p = 0,04/0,057 = 0,7. Аналогично и для остальных интервалов, результаты приведены в таблице 2.3

При построении графика дифференциального закона распределения (плотности распределения), который приведен на рисунке 2.3, надо учитывать, что абсциссы точек должны располагаться посередине каждого интервала, а ординаты будут соответствовать значению f (x) в указанном интервале.

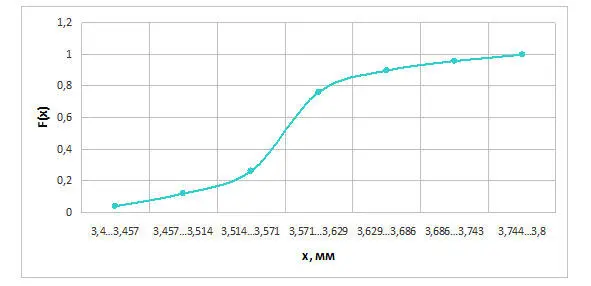
Рисунок 2.1 – Функция распределения

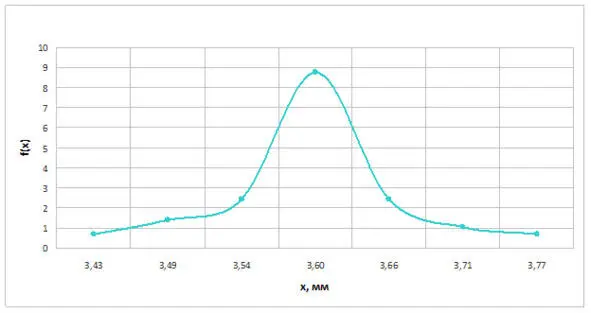
Рисунок 2.2 – Плотность распределения

Предварительно вид закона распределения можно определить и по внешнему виду гистограммы распределения, которая приведена на рисунке 2.3.

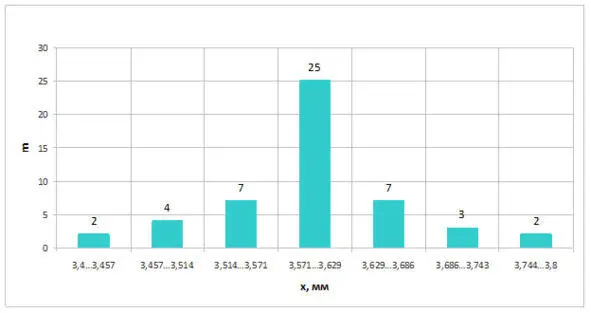
Рисунок 2.3 – Гистограмма распределения

Для дискретной случайной величины в том случае если она принимает небольшое количество значений, интервалы между которыми одинаковы (например она принимает только значения 3, 4, 5, 6, 7, 8, 9) то можно рассчитывать вероятность того что случайная величина примет конкретное значение, в этом случае продолжительность интервала Δх = 1. В обратном случае необходимо также производить разбивку на интервалы. Все остальные вычисления проводятся аналогично.