Михаил Левицкий - Карнавал молекул. Химия необычная и забавная

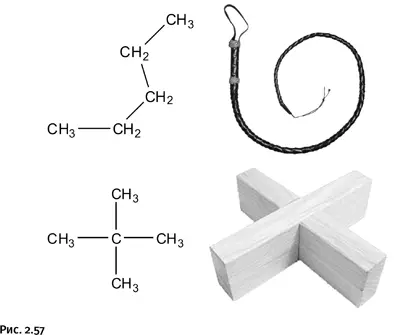
У химии свои взаимоотношения с энтропией. Например, она имеет количественную меру, ее размерность килоджоуль/градус, т. е. энергия, деленная на температуру (обычно указывают величину, приходящуюся на один моль вещества). Молекула каждого вещества имеет свою величину энтропии, которая зависит от того, насколько отдельные части молекулы и сама молекула подвижны при тепловых колебаниях. Чем больше возможных состояний, тем выше энтропия. Здесь играют роль упругость отдельных химических связей и валентных углов, а также общая форма молекулы. Например, у молекулы пентана CH3-CН2-СН2-СН2-СН3 возможны различные повороты пятого, т. е. «хвостового», атома С относительно первого атома – это гибкая плетка. Молекула изомерного пентана С(СН3)4 представляет собой жесткую конструкцию, гибкого хвоста нет, и потому ее энтропия ниже, чем у линейной молекулы (рис. 2.57).

Точно так же, как мы ранее определяли тепловой эффект реакции, значения энтропии веществ можно взять из справочника, они указаны в расчете на один моль вещества. Затем, суммируя энтропии продуктов реакции и вычитая сумму энтропий исходных соединений, можем узнать, каково изменение энтропии в процессе превращения. По существу, это простейшие арифметические вычисления.

Здесь будет уместно сказать, что для получения нужных для вычислений величин (энергии образования и энтропии) химики все реже пользуются справочниками, а обычно поручают это различным компьютерным расчетным программам, пользоваться которыми вполне по силам рядовому химику-синтетику. Дополнительное удовольствие химик получает от того, что может визуально наблюдать процесс расчета, в результате которого молекула приобретает оптимальную форму (энергетически выгодную), что отображается на мониторе в виде 3D-анимации. К тому же можно вычислить необходимые нам величины для соединений, которые пока не получены и существует лишь их формула, написанная на бумаге, а потому, естественно, сведения в справочниках отсутствуют.

Вновь вернемся к энтропии, точнее к ее изменению в процессе реакции. Иногда даже без вычислений, глядя только на схему реакции (например, на ту, которую предложил в самом начале нашего рассказа начинающий химик), можно сказать, что энтропия в результате этой реакции уменьшается. Все дело в том, что из двух молекул получается одна.

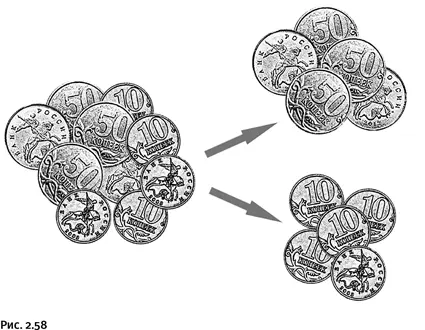
Приведем пример. Представьте небольшую кучку монет достоинством 10 коп. и 50 коп. Монеты располагаются неравномерно, т. е. случайным образом: где-то больше 10-копеечных монет, где-то 50-копеечных. Это система с высокой степенью беспорядка. Уменьшить его мы могли бы, если бы разделили содержимое кучки на две группы так, чтобы в каждой оказались монеты одинакового достоинства. В каждой полученной группе полного порядка все равно не было бы, одни монеты лежали бы вверх гербом, другие – решеткой, да и повернуты они по-разному. Тем не менее после разделения монет на две группы энтропия бы уменьшилась, т. е. порядка стало немного больше (рис. 2.58).

Процедура разделения монет на две группы мало похожа на химическую реакцию. Для того чтобы достичь сходства, поместим всю исходную кучку монет в мешочек и начнем встряхивать. Далее допустим, что при встряхивании монеты разного достоинства «слипаются» и из одной 50-копеечной и пяти 10-копеечных образуется рубль. В результате после долгого встряхивания в мешочке окажутся только рубли (если исходное соотношение 10- и 50-копеечных монет было 5:1). Теперь, очевидно, вам понятно, что энтропия содержимого в мешочке понизилась, стало меньше «беспорядка», поскольку получились только монеты одного достоинства и их количество меньше, чем было до встряхивания (рис. 2.59).

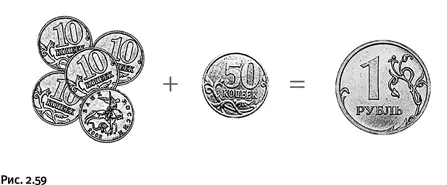
Рассмотренная ситуация с монетами очень напоминает реакцию получения уксусной кислоты из метана и углекислого газа, где из двух молекул получилась одна. Очевидно, что эта реакция проходит с уменьшением энтропии. Во многих случаях найденное нами правило сохраняется: если в правой части химического уравнения молекул меньше, чем в левой (стехиометрические коэффициенты, стоящие у реагентов, тоже учитывают), то реакция проходит с уменьшением энтропии. Естественно, если в правой части уравнения молекул больше, чем в левой, то энтропия в результате реакции, скорее всего, возрастает. На практике энтропийный фактор оценивают не на глазок, как это делали мы (с какой стороны уравнения участвует больше молекул), а по расчетам. Часто бывает, что в правой и левой части уравнения одинаковое количество молекул, в этом случае расчет становится необходимым.

Для рассматриваемой реакции проведенный расчет подтверждает наши предположения: энтропия в результате реакции снижается на величину 220 Дж/градус. Много это или мало? В нашем случае это не так существенно, поскольку важно лишь то, что она снижается, что создает для реакции непреодолимый барьер. На основании чего можно сделать такой категоричный вывод? Существует всего четыре правила, которые позволяют сказать, пойдет реакция или не пойдет. Мы с нашей реакцией попали в самую неудачную ситуацию.

Четыре правила для химика

Для того чтобы определить, возможно ли протекание реакции, надо сопоставить величину теплового эффекта и изменение энтропии. Существует всего четыре варианта.

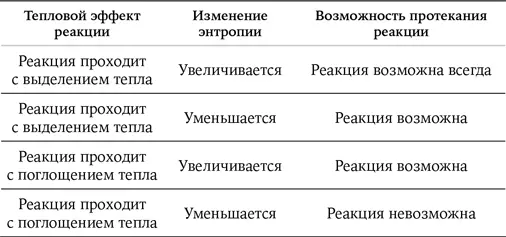
Расчеты показали, что наша реакция эндотермическая и к тому же идет с понижением энтропии, т. е. наш вариант – четвертый, а значит, реакция невозможна. Не помогут никакие катализаторы, давление, нагревание, охлаждение, перемешивание и все остальные лабораторные приемы.

А что представляют собой остальные три варианта в реальности? Для первого варианта наиболее убедительный пример – тринитротолуол (тол). Он может разлагаться со взрывом, реакция отчетливо экзотермическая. Кроме того, из одной молекулы тринитротолуола образуется по крайней мере четыре соединения – СО2, N2, NO, Н2О. Следовательно, энтропия возрастает. К этому же варианту относятся все процессы горения углеводородного топлива, в результате чего образуются газообразные продукты СО2 и Н2О.

Грустный четвертый случай мы уже рассмотрели, а два промежуточных наиболее интересны, поскольку чаще всего встречаются в химической практике. В обоих этих случаях надо сопоставить количественные величины теплового эффекта реакции и энтропии. Поскольку размерность теплового эффекта – калории, а у энтропии – калории/градус (в расчете на один моль вещества), то следует величину энтропии умножить на значение абсолютной температуры, при которой происходит процесс, после этого размерности станут одинаковыми и величины можно будет сравнивать. Обратите внимание, во втором и третьем варианте оба фактора действуют в противоположных направлениях. Во втором варианте выделение тепла способствует легкому протеканию реакции, а уменьшение энтропии делает ее менее вероятной. В третьем варианте оба фактора «меняются местами». Конечный результат зависит от того, кто кого перетянет.